And at the end of this page, the main ideas in these 9 sections
are condensed in the introductory Overview
of Scientific Method.
To learn about any part of the diagram, click on it.
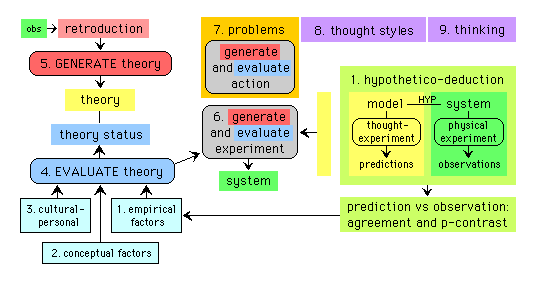
This diagram is a simplification of the full diagram for Integrated Scientific Method.
These links are all inside-the-page, even though (so they'll be easier to read)
they're not italicized.
Introduction: a disclaimer , coping with inconsistent terminology , the nine sections , and framework / elaboration.
note: ISM is an abbreviation for my model of Integrated Scientific Method.
1. Empirical Factors: experimental system , theories & models , supplementary theories , predictions , hypothetico-deductive logic , degree of agreement , degree of predictive contrast , previous and current hypotheses.
2. Conceptual Factors: 2A. Simplicity (logical systematicity , simplified models , coping with complexity , tensions between conflicting criteria , false but useful); 2B. Constraints on Components (preferences and motivations , constraints on unobservable components); 2C. Scientific Utility (theory structure and cognitive utility , alternative representations , simplification and cognition , a synthesis , cognitive utility and research utility , acceptance and pursuit , relaxed conceptual standards , utility in generating experiments , testability); 2D. External Relationships (overlapping domains and shared components , sharing a domain , external connections , levels of organization , theories with wide scope , external relationships viewed as internal relationships , unification as a goal of science , moving from description to explanation , consilience with simplicity , a narrowing of domains).
3. Cultural-Personal Factors: the joy of science , other psychological motives and practical concerns , metaphysical worldviews and ideological principles , opinions of "authorities" , social-institutional contexts , science affects culture and culture affects science , personal consistency and feedback , thought styles , over-generalizing , controversy.
4. Theory Evaluation: delay , intrinsic status and relative status , variable-strength conclusions and hypotheses , conflicts between criteria.
5. Theory Generation: selection and invention , retroduction and deduction , retroduction and hypothetico-deduction , domain-theories and system-theories , retroductive generalization , strategies for retro-generalizing , retroduction and induction , generation and evaluation , invention by revision , analysis and revision , internal consistency , external relationships.
6. Experimental Design (Generation-and-Evaluation): field studies , goal-directed design , learning about systems and theories , learning about experimental techniques , anomaly resolution , crucial experiments , heuristic experiments and demonstrative experiments , logical strategies for experimental design , vicarious experimentation , customized design , taking advantage of opportunities , thought-experiments in design , four contexts for thought-experiments.
7. Goals and Actions in Problem Solving: preparation , goal-constraints , secondary goals , primary goals , questions or objectives or problems , project formulation and decision , action generation and evaluation , conclusion , persuasion , 3Ps and 4Ps , interactions between stages and activities , interactions between and within levels.
8. Thought Styles: a definition , effects on observation and interpretation , conceptual ecology , a puzzle and a filter , the 4Ps and thought styles , variations , communities in conflict.
9. Productive Thinking: motivation , memory , creativity and critical thinking.
OVERVIEW of Scientific Method (at end of this page)
DIAGRAM of Scientific Method (at end of this page)
And a website I've recently developed (2012-present)
describes a
Design Process that includes Science Process.
Introduction
A DESERVEDLY HUMBLE DISCLAIMER. Compared with my description of science in the "overview of scientific method" page, this "details of scientific method" page is intended to be more complete, but not fully complete. Each topic in my elaboration has been studied for years (or even lifetimes) by numerous scholars. In many cases, ideas that I cover in a few paragraphs are the topic for an entire book, which can treat these ideas with greater detail and sophistication than in my brief summary.
TRYING TO COPE WITH INCONSISTENT TERMINOLOGY. In developing a model of Integrated Scientific Method (ISM), one major challenge was the selection of words and meanings. If everyone used the same terms to describe scientific methods, I would use these terms in ISM. Unfortunately, there is no consistent terminology. Instead, there are important terms — especially model, hypothesis, and theory — with many conflicting meanings, and meanings known by many names. Due to this inconsistency, I have been forced to choose among competing alternatives. Despite the linguistic confusion, over which I have no control, in the context of ISM I have tried to use terms consistently, in ways that correspond reasonably well with their common uses by scientists, philosophers, and educators. { details about terminology }
NINE SECTIONS. The framework of ISM is divided into nine sections: three for evaluation factors (empirical, conceptual, and cultural-personal), three for activities (evaluating theories, generating theories, and experimental design), and one each for problem solving, thought styles, and productive thinking. Sections 1-6 assume that during problem formulation there already has been the selection of an area of nature to study; and in Sections 1-4 and 6, there is already a theory about this area.
FRAMEWORK and ELABORATION. The "Goals of ISM" page makes a distinction between the ISM framework and an elaboration of this framework by myself or by others. The overview describes the ISM framework with minimal elaboration. In this "details" page there is lots of elaboration, but much of this is a discussion of concepts that I consider a part of the ISM framework because they are essential for accurately describing science. Therefore, the ISM framework includes everything in the overview, and more. Perhaps in the future I will try to define the precise content-and-structure of the ISM framework, but for now this definition remains flexible, partly because my own concept of the framework keeps changing as I continue to think about the methods used by scientists.
The following elaboration assumes the reader is familiar with the "Overview of Scientific Method" as background knowledge. As a reminder, and so you can easily review, at the beginning of each section there is a link to the corresponding description (located at the end of this page) from the overview. And at the end of each section there is a link to the Table of Contents at the top of this page.
REFERENCES. The references cited in this page are listed in another page.
1. Empirical Factors in Theory Evaluation
For a background foundation, read An Overview of Scientific Method, Section 1.
Theory evaluation based on observations, using hypothetico-deductive logic, is often considered the foundation of scientific method. I agree.
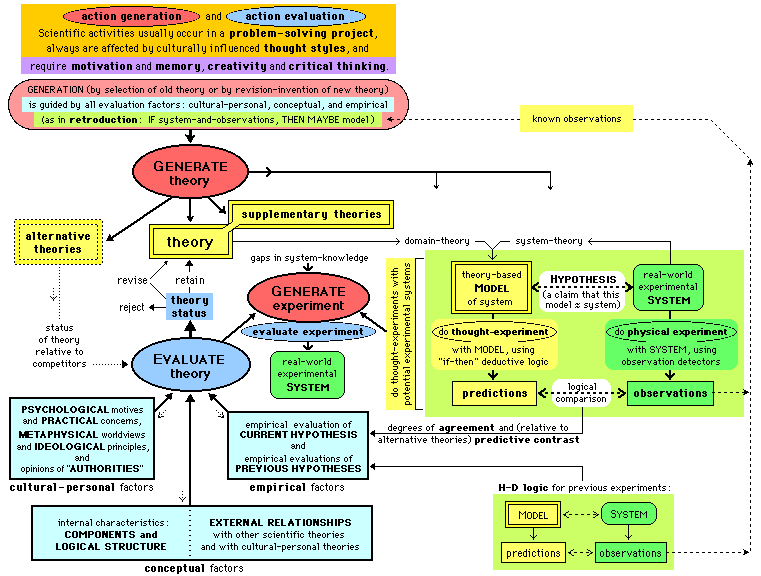
EXPERIMENTAL SYSTEM. In my model of Integrated Scientific Method (ISM), an experimental
system is defined as everything involved in an experiment. For example,
when x-rays are used to study the structure of DNA, the system includes the
x-ray source, DNA, and x-ray detector/recorder, plus the physical context (such
as the bolts and plates used to fix the positions of the source, DNA, and detector).
Data is often collected
more than once during an experiment. Early observations can measure initial
conditions that characterize the experimental system (such as x-ray wavelength,
and geometry of the source-DNA-detector setup) and are required to make predictions.
Later, to measure final conditions, scientists collect data (such as an
x-ray photograph) that is labeled "observations" in ISM.
THEORIES are humanly constructed representations
intended to describe or describe-and-explain a set of related phenomena in a
specified domain of nature.
An explanatory theory
guides the construction of models; each model
is a representation of a system's composition
(what it is) and operation (what it does).
Composition includes a model's parts and their organization into larger structures.
Operation includes the actions of parts (or structures) and the interactions
between parts (or structures).
With a descriptive
theory, a model describes only observable
properties and their relationships, and makes predictions about observable properties.
A model can include a partial composition-and-operation description of a system,
but this is not required as a necessary function of the theory.
An example of a descriptive theory is Newton's
theory of gravitational force, which does postulate compositional entities (bodies
with mass) and causal interactions (each body exerts an attractive force on
the other), but does not describe a mechanism for the interactions that cause
the force, even though (using its equation, F = GMm/rr) it can make predictions
that are usually quite accurate.
An example of an explanatory theory is atomic
theory, which postulates unobservable entities (protons, electrons,...) and
interactions (nuclear, electromagnetic,...) in an effort to explain observable
properties. Questions about the legitimacy of postulating "unobservables"
has been one source of conceptual constraints for the types of components used
in scientific theories.
It can be useful to distinguish between descriptive
and explanatory theories, even though there is no distinct line; Newton's theory
explains some, and atomic theory does not explain all. And my simple treatment
here is only a summary of the more sophisticated analyses by philosophers who
try to define what constitutes a satisfactory explanation in science.
SUPPLEMENTARY THEORIES include, but are not limited
to, theories used to interpret observations. Shapere (1982) analyzes an
"observation situation" as a 3-stage process in which information
is released by a source, is transmitted, and is received by a receptor, with
scientists interpreting this information according to their corresponding theories
of the source, the transmission process, and the receptor.
The label "supplementary" is based
on assumptions about goals. For example, in the early 1950s when "DNA
chasers" were generating and evaluating theories for DNA structure, this
DNA theory was the main theory, while theories
about x-rays (including their generation, transmission, interaction with DNA,
and detection) were the supplementary theories.
But these x-ray theories — in a different context, during an earlier period
of science when the main goal was to develop x-ray theories — were considered
to be the main theories.
PREDICTIONS. By using a model that is
based on a specified experimental system and relevant theories (main + supplementary), scientists can make predictions in more
than one way: by logical deduction beginning with a composition-and-operation
model, by making model-based calculations, by "running a model" mentally or in a computer
simulation, or by inductive logic that assumes the results will be similar to
those in previous experiments with similar systems. If predictions can
be made in several ways for the same system, this will serve as a cross-check
on the predictions and on the predicting methods. {more on thought experiments}
It can be useful to think of combining two
sources — a general domain-theory (that
applies to all systems in a domain) and a specific system-theory
(about the characteristics of one system, including its initial
system-conditions) — in order to predict the final
system-conditions. Thinking in terms of a domain-theory
and a system-theory is also useful for the retroductive
generation of ideas
for a theory. { In additon to this link for "retroductive generation...", here are two more: my Introduction to Scientific Method has an overview-summary of how we make predictions; and a condensed 4-paragraph summary, describing experimental systems and how theories (explanatory or descriptive, at the levels of a general domain or specific system) can be used to construct
a model
and
make
predictions,
is in my Overview of Scientific Method. }
HYPOTHETICO-DEDUCTIVE LOGIC is represented, in the
ISM diagram, with a box (adapted from Giere, 1991) whose dual-parallel shape
symbolizes two parallel relationships -- between mental
and physical experiments, and between model-system
and prediction-observation similarities. This logic gets
its name by combining hypothetico (from the top
of the box) with deductive (from the left side
of the box). { The ISM definitions for model and hypothesis are also adapted from Giere (1991). }
Since predictions can be made using deductive
logic and also inductive logic, should we also think about the characteristics
and uses of "hypothetico-inductive" logic? Typically, during
"if-then logic" based on an explanatory model (that proposes a composition
and operation), what are the relative contributions of deduction and induction?
And when we generalize by using the inductive logic that "if systems are
similar, then observations will be similar," how much deductive logic is
being used when we try to estimate how "similarities and differences in
systems" will translate into "similarities and differences in observations"?
These questions are interesting, and they will be pursued more thoroughly at
a later time.
DEGREE OF AGREEMENT. In formal logic,
"deductive" inference implies certainty. But in scientific hypothetico-deduction,
deductive inference often produces probabilistic predictions. For example,
a genetics theory may predict that 25% of offspring will have a recessive variation
of a trait.
Often, observation also involves uncertainties,
such as random fluctuations; and data collection may involve subjective decisions
such as assigning specimens into categories. For many experiments, a reliable
estimate for degree of agreement requires the use of sophisticated techniques
for data analysis that take into account the sample size, variability, and representativeness,
and the statistical nature of predictions and observations. These techniques
produce a probabilistic answer, not a simple yes or no. For example, scientists
could estimate the agreement for a theory that a certain variation is recessive,
when 4 of 20 offspring (instead of the predicted 5-of-20) have this variation.
For example, consider a theory that Chicago is in Wisconsin, which produces the deductive prediction that "if Chicago is in Wisconsin, then Chicago is in the United States." When a geographer confirms that Chicago is in the U.S., does this prove the theory is true? No, because alternative theories, such as "Chicago is in Illinois" and "Chicago is in Iowa," make the same correct prediction.
Another example is used by Sober (1991), who describes one way to test a theory that John is an Olympic weightlifter; you ask John to lift a hat. The Olympic Weightlifter Theory (OW) predicts that he can lift the hat, and he does. But plausible alternative theories (like "John is a 98-pound weakling, not an Olympic weightlifter") predict the same result, so this experiment offers little support for OW despite its correct prediction.
In an effort to cope with the logical limitations of considering only agreement, a scientist can ask any of five roughly equivalent questions:
"Was the prediction likely to agree with the data even if the model under consideration does not provide a good fit to the real world?" (Giere, 1991, p. 38)
Would the results be surprising if the model was not a good representation of the system? (this question applies the "Surprise Principle" of Sober, 1991)
Should an agreement between predictions and observations elicit a response of "So what?" or "Wow!"?
To what extent does the experiment provide a crucial test that can discriminate between this theory and alternative theories?
What is the degree of contrast between the predictions of this theory and the predictions of plausible alternative theories?
For any experiment, a degree of predictive
contrast can be estimated by asking one or more of these five questions.
For example, the results of the hat-lifting experiment are likely to occur even
if OW is false, so we wouldn't be surprised by this observation even if OW was
false, and a response of "so what" is justified; the experiment does
not discriminate between theories, because there is no contrast between the
predictions of OW and the predictions of plausible alternative theories.
A consideration of predictive contrast is
useful because it functions as a counterbalance to the skeptical principle that
a theory is not proved by agreement between predictions and observations.
Despite the impossibility of proof, the status of a theory increases when it
is difficult to imagine any other plausible theory that could make the same
correct predictions. Of course, an apparent lack of alternative explanations
could be illusory, due to a lack of imagination, but scientists usually assume
that a high degree of predictive contrast increases the justifiable confidence
in a claim that there is a connection between a prediction-observation agreement
and a model-system similarity.
PREVIOUS AND CURRENT HYPOTHESES. An empirical evaluation should include all experiments, past and present, that seem relevant for achieving the goals of the evaluators. When they generate a theory from multiple sources of data, scientists use art and logic.
2. Conceptual Factors in Theory Evaluation
An Overview of Scientific Method, Section 2
A theory is constructed
from components that are propositions used to describe empirical patterns [in
a descriptive theory] or to construct composition-and-operation models [in an
explanatory theory] for a system's composition (what it is) and operation (what
it does).
ISM (Integrated Scientific Method) follows Laudan (1977) in making a distinction
between empirical factors and conceptual factors, and between conceptual factors
that are internal and external. Internal conceptual factors (regarding
components and logical structure) involve the characteristics and logical interrelationships
of a theory's own components, while external conceptual factors are the external
relationships between a theory's components and the components of other theories
(either scientific or cultural-personal). Because this is such a long
section, it is split into four parts: three to discuss internal characteristics
(simplicity, constraints, utility), and one for external relationships.
2A. Simplicity
LOGICAL SYSTEMATICITY. To illustrate logical
structure, Darden (1991) compares two theories that claim to explain the same
data; T1 contains an independent theory component for every data point, while
T2 contains only a few logically interlinked components. Even if both
theories have the same empirical adequacy, most scientists will prefer T2 due
to its logical structure.
When one component is not logically connected
to other components, it is usually considered an ad hoc
appendage that makes a theory less logically systematic and less desirable.
If scientists perceive T1 as an inelegant patchwork of ad hoc components that
have no apparent function except to achieve empirical agreement with old data,
they will not be impressed with T1's predictions, and will they not expect T1
to successfully predict new data.
Another perspective: T1 has specialized components, by contrast with the generalized components of T2.
Internal consistency,
with logical agreement among a theory's components, is highly valued.
Systematicity is weakened by an independence of components (with no relationships)
as in T1, but inconsistency among components (with bad relationships) is the
ultimate non-systematicity.
SIMPLIFIED MODELS. Even though a complete model of a real-world experimental system would have to include everything in
the universe, a more useful model is obtained by constructing a simplified
representation that includes only the relevant entities and interactions,
omitting everything whose effect on the outcome is considered negligible.
For example, when scientists construct a
model for a system of x-rays interacting with DNA, they will ignore (implicitly,
without even considering the possibility) the bending of x-rays that is caused
by the gravitational pull of Pluto. Or scientists can make an explicit
decision to simplify a model.
One simplifying strategy is to construct
a family of models (Giere, 1988) that are variations
on a basic theme. For example, we could begin with Newtonian Physics, and simplify its application by constructing a stripped-down model of a system. When applying Newton's
Theory to a falling ball, a stripped-down model might ignore the effects of
air resistance, and the change in gravitational force as the ball changes altitude.
For some purposes this simplified model is sufficient to make a calculation (a prediction) with satisfactory accuracy. And if scientists
want a more complete model, they can include one or more “correction factors”
that previously were ignored. The inclusion of different correction factors produces
a family of related models with varying degrees of completeness, each useful for a different
situation and objective.
For example, if a bowling ball is dropped
from a height of 2 meters, ignoring air resistance will allow calculation-predictions that are satisfactory for almost all purposes. But when a tennis ball falls 50 meters, if air resistance is ignored the predictions
are significantly inaccurate. And a rocket
will not make it to the moon based on models (used for making calculation-predictions)
that do not include air resistance and the variation of gravity with altitude.
In comparing these situations there are two major variables: the weighting
of factors (which depends on goals), and degrees of predictive contrast. Weighting of factors: for the moon rocket a demand for empirical accuracy
is more important than the advantages of conceptual simplicity, but for most
bowling ball scenarios the opposite is true. Predictive contrast:
for the moon rocket there is a high degree of predictive contrast between alternative
theories (one theory with air resistance and gravity variations, the other without)
and the complex theory makes predictions that are more accurate; but for the
bowling ball there is a low degree of predictive contrast between these theories,
so empirical evaluation does not significantly favor either model.
COPING WITH COMPLEXITY. A common strategy for developing a simple theory about a complex system is to tolerate a reduction in empirical adequacy. For example, Galileo was able to develop a mathematical treatment of physics because he was willing to relax the constraints imposed by demands for empirical accuracy; he did not try to obtain an exact agreement with observations. His approach to theorizing — by focusing on the analysis of imaginary idealized systems — was controversial because Galileo and his critics disagreed about the fundamental goals of science, because Galileo challenged the traditional criterion that exact empirical agreement was a necessary condition for an adequate theory. In this area, Galileo and his critics disagreed about a fundamental goal of science.
TENSIONS BETWEEN CONFLICTING CRITERIA.
These conflicts are common. For example, in a famous statement of simplicity
known as Occam's Razor — "entities should not be multiplied, except from
necessity" — a preference for ontological economy ("entities should
not be multiplied") can be overcome by necessity. But evaluation
of necessity, such as judging whether a theory revision is improvement
or ad hoc tinkering, is often difficult, and may require a deep understanding
of a theory and its domain of application, plus sophisticated analysis.
A common reason for non-simplicity is a
desire for empirical adequacy, since including additional components in
a theory may help
it predict observations more accurately and consistently. Another reason
is to construct a more complete model for the composition-and-operation of
systems.
Sometimes, however, there is a decision
to decrease completeness in order to achieve certain types of goals. In
this situation, although scientists know their model is being made less complete,
whatever loss occurs due to simplification
(and it may not be much) is compared with the benefits gained, in an attempt
to seek a balance, to construct a theory that is optimally accurate-and-useful. Potential
benefits of simplification may include an increase in cognitive utility by making a model easier to learn and use, or
by focusing attention on the essential aspects of a model.
If it is constructed skillfully, with wise
decisions about including and excluding components, a theory that is more complete
is usually more empirically adequate. But not always. A model can
be over-simplified by omitting relevant factors that should be included, or
it can be over-complicated by including factors that could be omitted, or should be omitted.
Due to the possibility of "...should...", sometimes simplifying a complex model will produce
a model that makes more accurate predictions for new experimental systems, as
explained by Forster & Sober (1994).
FALSE BUT USEFUL. Wimsatt (1987)
discusses some ways that a false model can be scientifically useful. Even
if a model is wrong in some ways, it may inspire the design of interesting experiments.
It may stimulate new ways of thinking that lead to the critical examination
and revision (or rejection) of another theory. It may stimulate a search
for empirical patterns in data. Or it may serve as a starting point for further development; by
continually refining and revising a false model, perhaps a better model can
be developed.
Many of Wimsatt's descriptions of utility
involve a model that is false (i.e. not totally true) due to an incomplete composition-and-operation description of components
for entities, actions, or interactions. When the erroneous predictions
of an incomplete model are analyzed, this can provide information about the
effects of components that have been omitted or oversimplified. For example,
to study how "damping force" affects pendulum motion, scientists can
design a series of experimental systems, and for each system they compare their
observations with the predictions of several models (each with a different characterization
of the damping force); then they can analyze the results, in order to evaluate
the advantages and disadvantages of each characterization. Or consider
the Castle-Hardy-Weinberg Model for population genetics, which assumes an idealized
system that never occurs in nature; deviations from the model's predictions
indicate possibilities for evolutionary change in the gene pool of a population.
2B. Constraints on Components
PREFERENCES and MOTIVATIONS. Scientific communities develop preferences for the types of components that should (and should not) be used in a theory. For example, prior to 1609 when Kepler introduced elliptical planetary orbits, it was widely believed that in astronomical theories all motions should be in circles with constant speed. This belief played a role in motivating Copernicus:
In every field there are implicit and explicit constraints on theory components -- on the types of entities, actions and interactions to include in a theory's models for composition and operation. These constraints can be motivated by beliefs about ontology (after asking "Does it exist?") or utility (by asking "Will it be useful for doing science?"). For example, an insistence on uniform circular motion could be based on the ontological belief that celestial bodies never move in noncircular motion, or on the utilitarian rationale that using noncircular motions makes it more difficult to do calculations.
CONSTRAINTS ON UNOBSERVABLE COMPONENTS.
A positivist believes that scientific theories
should not postulate the existence of unobservable entities, actions, or interactions.
For example, behaviorist psychology avoids the concept of "thinking"
because it cannot be directly observed. A strict positivist will applaud
Newton's theory of gravitation, despite its lack of a causal explanatory mechanism,
because it is an empirical generalization that is reliable and approximately
accurate, and it does not postulate (as do more recent theories of gravity)
unobservable entities such as fields, curved space, or gravitons. But
most scientists, although they appreciate Newton's descriptive theory for what
it is, consider the absence of explanation to be a weakness.
some comments about terminology: Positivism
was proposed in the 1830s by Auguste Comte, who was motivated partly by anti-religious
ideology. In the early 20th century a philosophy of logical
positivism was developed to combine positivism with other ideas.
In current use, "positivism" can be used in a narrow sense (as Comte
did, and as I do here) or it can refer to anything connected with logical
positivism, including the "other ideas" and more. Logical
positivism can also be called logical empiricism. { Notice that empiricism
(i.e., positivism) is not the same as empirical.
A theory that is non-empiricist (because
it contains some components, such as atoms or molecules, that are unobservable)
can make
predictions about empirical data that can
be used in empirical evaluation. }
Although positivism (or empiricism, the name
typically given to current versions) is considered a legitimate perspective
in philosophy, it is rare among scientists, who welcome a wide variety of ways
to describe and explain. Many modern theories include unobservable entities
and actions, such as electrons and electromagnetic force, among their essential
components. Although most scientists welcome a descriptive theory that
only describes empirical patterns, at this point they think "we're not
there yet" because their limited theory is seen as just a temporary stage
along the path to a more complete theory. This attitude contrasts with
the positivist view that a descriptive theory should be the ending point for
science.
The ISM framework includes two
types of theories (and corresponding models) — descriptive and explanatory
— so it is compatible with any type of scientific theory, whether it is descriptive,
explanatory, or has some characteristics of each. My own anti-positivist
opinions, which are not part of the ISM framework, are summarized in the preceding
paragraph, and are discussed in more depth on a page that asks Should
Scientific Method be Eks-Rated?
2C. Scientific Utility
Theory evaluation can focus on plausibility or utility by asking "Is the theory an accurate representation of nature?" or "Is it useful?" This section will discuss the second question by describing scientific utility in terms of cognitive utility (for inspiring and facilitating productive thinking about a theory's components and applications) and research utility (for stimulating and guiding theoretical or experimental research). Theory evaluation based on utility is personalized -- it will depend on point of view and context, because goals vary among scientists, and can change from one context to another.
THEORY STRUCTURE and COGNITIVE UTILITY. Differences in theory structure can produce differences in cognitive structuring and problem-solving utility, and will affect the harmony between a theory and the thinking styles — due to heredity, personal experience, and cultural influence — of a scientist or a scientific community. If competing theories differ in logical structure, evaluation will be influenced by scientists' affinity for the structure that more closely matches their preferred styles of thinking.
ALTERNATIVE REPRESENTATIONS. Even for
the same theory, representations can differ. For example, a physics theory
can symbolically represent a phenomenon by words (such as saying “the earth orbits
the sun in an approximately elliptical orbit”), a visual representation
(a diagram or animation depicting the sun and the orbiting earth), or an equation
(using mathematical symbolism for objects, interactions, and actions). More generally,
Newtonian theory can be described with simple algebra (as in most introductory
courses), by using calculus, or with a variety of advanced mathematical techniques
such as Hamiltonians or tensor analysis; and each mathematical formulation can
be supplemented by a variety of visual and verbal explanations, and illustrative
examples. Similarly, the same theory of quantum mechanics can be formulated
in two very different ways: as particle mechanics by using matrix algebra, or
as wave mechanics by using wave equations.
Although two formulations of a theory may
be logically equivalent, differing representations will affect how the theory
is perceived and used. There will be differences in the ease of translation
into mental models (i.e., in ease of learning), in the types of mental models
formed, and in approaches to problem solving. Often, cognitive utility
depends on problem-solving context. For example, an algebraic version
of Newtonian physics may be the easiest way to solve a simple problem, while
a Hamiltonian formulation will be more useful for solving a complex astronomy
problem involving the mutually influenced motions of three celestial bodies.
Or consider how an alternate representation — made by defining the mathematical
terms "force x distance" and "mvv/2" as the verbal terms
"work" and "energy" — allows the cognitive flexibility
of being able to think in terms of an equation or a work-energy conversion,
or both.
SIMPLIFICATION and COGNITION. If a
theory is formulated at differ levels of simplification, these representations
will differ in both logical content and cognitive utility. A more complete
representation will (if the mind can cope with it) produce mental models that
are more complete; and in some contexts these models will be more useful for
solving problems. But in other contexts a simpler formulation may be more
useful. For example, a simpler model may help to focus attention on those
features of a system that are considered especially important.
In designing models that will be used by
humans with limited cognitive capacities, there is a tension between the conflicting
requirements of completeness and simplicity. It is easier for our minds
to cope with a model that is simpler than the complex reality. But for
models in which predicting or data processing is done by computers, there is
a change in capacities for memory storage and computing speed, so the level
and nature of optimally useful complexity will change. High-speed computers
can allow the use of models — for numerical analysis of data, or for doing
thought-experiment simulations (of weather, ecology, business,...) — that would
be too complex and difficult if computations had to be done by a person.
A SYNTHESIS? Philosophy of science and cognitive psychology overlap in areas such as the structuring of scientific theories (studied by philosophers) and the structuring and construction of mental models (studied by psychologists). Research in this exciting area of synthesis is currently producing many insights that are helping us understand the process of thinking in science, and that will be useful for improving education.
COGNITIVE UTILITY and RESEARCH UTILITY. These two aspects of SCIENTIFIC UTILITY are related, because Cognitive Utility is important for promoting Research Utility, making a theory useful for doing research.
ACCEPTANCE and PURSUIT. Laudan (1977) observes that even when a theory has weaknesses, and evaluation indicates that it is not yet worthy of acceptance (of being treated as if it were true), scientists may rationally view this theory as worthy of pursuit (for exploration and development by further research) if it shows promise for stimulating new experimental or theoretical research:Laudan suggests that when scientists judge whether a theory is worthy of pursuit, instead of just looking at its momentary adequacy, they study its rate of progress and potential for improvement. Making a distinction between acceptance and pursuit is useful when thinking about scientific utility, because a theory can have a low status for acceptance, but a high status for pursuit. If a theory is judged to be worthy of pursuit but not acceptance, it needs development but it shows enough promise to be considered worth the effort.
RELAXED CONCEPTUAL STANDARDS. According to Darden (1991) it may be scientifically useful to evaluate mature and immature theories differently. In a mature theory, scientists typically want components to be clearly defined and logically consistent. But in an immature theory that is being developed, there are advantages to temporarily relaxing expectations for clarity and consistency:For a developing theory, some criteria are less rigorous, but other characteristics — such as a flexibility that allows easy revision, and extendability for adapting to a widening domain — may be more important than in a mature theory.
UTILITY IN GENERATING EXPERIMENTS. A new theory can promote research by offering a new perspective on the composition and operation of experimental systems, and by inspiring ideas for new systems and techniques. { Of course, even after a theory has passed through the pursuit phase and is generally accepted, there may be opportunities for experimenting (to explore the old theory's application for new systems) and theorizing. But often the opportunities for exciting research are more plentiful with a new theory. }
TESTABILITY. Usually, to stimulate experimentation a theory must predict observable outcomes. Even when theory components are unobservable and thus cannot be tested by direct observation, they can be indirectly tested if they make predictions about observable properties. These predictions fulfill the practical requirement, in hypothetico-deductive logic, for testability -- which requires predictions that can be compared with observations. Testability is useful for scientifically evaluating a theory's plausibility, but it is not logically related to whether or not a theory is true. And even if a theory is not empirically testable, it can be scientifically useful if it contributes to a more accurate critical evaluation of other theories.
2D. External Relationships
OVERLAPPING DOMAINS and SHARED COMPONENTS. The external relationships between scientific theories can be defined along two dimensions: the overlap between domains, and the sharing of theory components. If two theories never make claims about the same experimental systems, their domains do not overlap; if, in addition, the two theories do not share any components for their models, then these theories are independent. But if there is an overlapping of domains or a sharing of components, or both, there will be external relationships.
SHARING A DOMAIN. If two theories with overlapping domains construct different models for the same real-world experimental system, these are alternative theories in competition with each other, whether or not they differ in empirical predictions about the system. In this competition, the intensity of conceptual conflict increases if there is a large overlap of domains, and a large difference in components for models. { There can also be conflict (which may or may not be conceptual) if there is a contrast in predictions. }Usually, as in the case of oxidative phosphorylation, one theory emerges as the clear winner after a period of conflict. But not always. For example,
Of course, a declaration that "both factors contribute to speciation"
is not the end of inquiry. Scientists can still analyze an evolutionary
episode to determine the roles played by each factor. They also can debate
the importance of each factor in long-term evolutionary scenarios involving
many species. And there can be an effort to develop theories that more
effectively combine these factors and their interactions.
A different type of coexistence occurs with
Valence Bond theory and Molecular Orbital theory, which use different types
of simplifying approximations in order to apply the core principles of quantum
mechanics for describing the characteristics of molecules. Each approach
has advantages, and the choice of a preferred theory depends on the situation:
on the molecule being studied, and the objectives; the abilities, experience,
and thinking styles of scientists; or the computing power available for
numerical analyses. Or perhaps both theories can be used. In many
ways they are complementary descriptions, as in "The Blind Men and the
Elephant," with each theory providing a useful perspective. This
type of coexistence (where two theories provide two perspectives) contrasts
with the coexistence of causal factors in speciation (where two theories propose two potential co-agents
in causation) and with the non-coexistence in oxidative phosphorylation (where
one theory has vanquished its former competitors).
SHARING A COMPONENT. The preceding
subsection describes the competition that occurs when two theories construct
different models for the same system. By contrast, in this subsection
the same type of theory component is used in models constructed for different
systems.
Even if two theories do not claim the same
domain, there is conflict if both theories contain the same type of component
but disagree about its characteristics. For example, in the late 1800s
a thermodynamic theory, based on the earth's rate of cooling, contained a component
for time; and this time had to be less than 100 million years, in order to correctly
predict the known observations. But theories in geology and evolutionary
biology constructed theories that required, as an essential component, an earth
that is much older than this time interval.
For awhile this conflict motivated adjustments,
mainly for theories in geology and biology. But in 1903 the discovery
of radioactive decay radioactive decay — which provides a large source of energy
to counteract the earth's cooling — modified the characterization of the earth
as an experimental system. With this newly revised system and the unchanged
theory of thermodynamics, a calculation showed the earth to be much older, consistent
with the original theories in geology and biology.
When two or more theories are in conflict,
as described above, there is a conceptual difficulty for all of the theories,
but especially for those in which scientists have less confidence. Conversely,
agreement about the characteristics of shared components can lend support to
these components. For example, many currently accepted theories contain,
as an essential component, time intervals of long duration. Physical processes
occur during this time, and these processes are necessary for empirical adequacy
in explaining observations; if the time-component is changed to a shorter time
(such as the 10,000 years suggested by young-earth creationists) the result
will be erroneous predictions about a wide range of phenomena. Theories
containing an old-earth component span a wide range, with domains that include
ancient fossil reefs, sedimentary rock formations (with vertical changes), seafloor
spreading (with horizontal changes) and continental drift, magnetic reversals,
radioactive dating, genetic molecular clocks, paleontology, formation and evolution
of stars, distances to far galaxies, and cosmology.
In a wide variety of theories, the same type
of component (for amount of time) always has the same general value: a very
long time. This provides support for the shared component — an old earth
(and an old universe) — and this support increases because an old earth is
an essential component of many theories that in other ways, such as the domains
they claim and the other components they use, are relatively independent.
This independence makes it less likely — compared with a situation where two
theories are closely related and share many essential components, or where the
plausibility of each theory depends on the plausibility of the other theory
— that suspicions of circular reasoning are justified. { Of course,
the relationships that do exist between these old-earth theories can be considered
when evaluating the amount of circularity in the support claimed for the shared
component. }
But in these theories, is the age of the earth a component or a conclusion? It depends on perspective. In most cases the age can be viewed as a conclusion reached by "solving an equation" (such as the one describing the earth's rate of cooling) for time; all of the theories claim to describe the same type of phenomenon (involving time), so they share a domain rather than a component. But it also makes sense to think of time as a component because, in each case, time is one aspect of a theory whose main goal is to explain the phenomenon being studied — a fossil reef, rock formation, seafloor spreading,... — not to explain the time. Or perhaps the long time-interval can be viewed as a supplementary theory that in each area is needed to produce adequate models. With any of these perspectives, the conclusion (of strong support for a long period of time) is similar.
EXTERNAL CONNECTIONS. In each example above, there was a connection between theories due to an overlapping domain or a shared component. The remainder of this subsection will examine different types of connections between theories, and the process of trying to create connections between theories.
LEVELS OF ORGANIZATION. Theories with a shared component can differ in their level of organization, and in the function of the shared component within each theory. For example, biological phenomena are studied at many levels — molecules, cells, tissues, organs, organisms, populations, ecological systems — and each level shares components with other levels. Cells, which at one level are models constructed from smaller molecular components, can function as components in models for the larger tissues, organs, or organisms that serve as the focus for other levels. Or, in a theory of structural biochemistry an enzyme might be a model (with attention focused on the enzyme's structural composition) that is built from atomic components and their bonding interactions, while in a theory of physiological biochemistry this enzyme (but now with the focus on its operations, on its chemical actions and interactions) would be a component used to build a model.
THEORIES WITH WIDE SCOPE. Another
type of relationship occurs when one theory is a subset of another theory, as
with DNA structure and atomic theory. During the development of a theory
for DNA structure, scientists assumed the constraint that DNA must conform to
the known characteristics of the atoms (C, H, O, N, P) and molecules (cytosine,...)
from which it is constructed. When Watson and Crick experimented with
different types of physical scale models, they tried to be creative, yet they
worked within the constraints defined by atomic theory, such as atom sizes,
bond lengths, bond angles, and the characteristics of hydrogen bonding.
And when describing their DNA theory in a 900-word paper (Watson & Crick,
1953) they assumed atomic theory as a foundation that did not need to be explained
or defended; they merely described how atomic theory could be used to explain
the structure of DNA.
There is nothing wrong with a narrow-scope
theory about DNA structure, but many scientists want science to eventually construct
"simple and unified" mega-theories with wide scope, such as atomic
theory. Newton was applauded for showing that the same laws of motion
(and the same gravitational force) operate in a wide domain that includes apparently
unrelated phenomena such as an apple falling from a tree and the moon orbiting
our earth, thus unifying the fields of terrestrial and celestial mechanics.
And compared with a conjunction of two independent theories, one for electromagnetic
forces and another for weak forces, a unified electro-weak theory is considered
more elegant and impressive due to its wide scope and simplifying unity.
EXTERNAL RELATIONSHIPS viewed as INTERNAL RELATIONSHIPS.
By analogy with a theory composed of smaller components, a unified mega-theory
is composed of smaller theories. And just as there are internal relationships
between components that comprise a theory, by analogy there are internal relationships
between theories that comprise a mega-theory. But these relationships
between theories, which from the viewpoint of the mega-theory are internal,
are external when viewed from the perspective of the theories. In this
way it is possible to view external relationships as internal relationships.
This treatment assumes that it can be useful
(even if sometimes difficult) to distinguish between levels of theorizing --
between components, sub-theories, theories, and mega-theories. When these
distinctions are made, in some cases the same types of relationships that exist
between two lower levels (such as components and sub-theories) will also exist
between other levels (such as components and theories, sub-theories and theories,
or theories and mega-theories).
I have found the analogy between internal
and external relationships to be useful for thinking about the connections between
levels of theorizing. At a minimum, it has prevented me from becoming
too comfortable with the labels "internal" and "external".
And when these simple labels no longer seem sufficient, there is a tendency
for thinking to become less dichotomous, which often stimulates a more flexible
and careful consideration of what is really involved in each relationship.
This heightened awareness is especially useful when considering the larger questions
of how theories relate to each other and interact to form the structure of a
scientific discipline, and how disciplines interact to form the structure of
science as a whole.
UNIFICATION AS A GOAL OF SCIENCE. It is doubtful whether constructing a Grand Unified Theory of Everything — so that eventually sociology can be explained in terms of elementary particle physics — is possible (O'Hear, 1989). And it is rarely a worthy goal in terms of scientific utility; at the present time, in most fields, most scientists will perform more useful research if they are not working directly on constructing a mega-theory to connect all levels of science. But making connections at low and intermediate levels of theorizing can be practical and important.
MOVING FROM DESCRIPTION TO EXPLANATION.
Often, a known empirical pattern is converted into an explanatory theory when
a composition-and-operation mechanism is proposed. For example,...
Newton's
physics explained the earlier descriptive theory of Kepler, regarding the elliptical
orbits of planets.
Another descriptive theory, the Ideal Gas Law (with
PV = nRT), was later explained by deriving it from Newtonian statistical mechanics.
And the structure of the Periodic Table, originally derived in the late 1800s
by inductive analysis of empirical data for chemical reactivities, with no credible
theoretical mechanism to explain it, was later derived from a few fundamental
principles of quantum mechanics. Explaining the Periodic Table was not
the original motivation for developing quantum theory; instead, it was
a pleasant surprise that provided support for the newly developed theory.
And because quantum mechanics also explained many other phenomena, over a wide
range of domains, it has served as a powerful unifying theory.
CONSILIENCE WITH SIMPLICITY. The previous paragraph describes how we can derive the Periodic Table's structure in two very different ways, by chemical properties and by quantum mechanics. This is an example of consilience. Another perspective on consilience is viewing it as a way to define the size-and-variety
of a theory's domain, in terms of the different "classes of facts"
(not just the number of facts) explained by this theory. Making a useful
estimate of consilience often requires sophisticated knowledge of a domain,
because it requires categorizing raw data into classes, and judging the relative
importance of these classes, and their differences.
Usually scientists want to increase the consilience
of a theory, but this is less impressive when it is done by sacrificing simplicity.
An extreme example of ad hoc revision was described earlier; theory T1
achieves consilience over a large domain by having an independent theory component
for every data point in the domain. But defining a collection of unrelated
components as "a theory" is not a way to construct a simple consilient
theory, and scientists are not impressed by this type of pseudo-unification.
There is too much room for wiggling and waffling, so each extra component is
viewed as a new "fudge factor" tacked onto a weak theory.
By contrast, consider Newton's postulate
that the same gravitational force, governed by the same principles, operates
in such widely divergent systems as a falling apple and an orbiting moon.
Newton's bold step, which achieved a huge increase in consilience without any
decrease in simplicity, was viewed as an impressive unification.
Although "consilience with simplicity"
can be a useful guideline, it should be used wisely. Simplicity is not
the only virtue (and sometimes it is not a virtue at all), so the unique characteristics
of each situation should be carefully considered when judging the value of an
attempted unification.
A NARROWING OF DOMAINS. Sometimes,
instead of seeking a wider scope, the best strategy is to decrease the size
of the domain claimed for a theory.
For example, in 1900 when Mendel's theory
of genetics was rediscovered, it was assumed that a theory of Mendelian Dominance
applied to all traits for all organisms. But further experimentation showed
that for some traits the predictions made by this theory were incorrect.
Scientists resolved these anomalies, not by revising their theory, but by redefining
its scope in order to place the troublesome observations outside the domain
of Dominance. Their initial theory was thus modified into a sub-theory
with a narrower scope, and other sub-theories were invented for parts of the
original domain not adequately described by Dominance. Eventually, these
sub-theories were combined to construct an overall mega-theory of genetics that,
compared with the initial theory of dominance, had the same wide scope, with
greater empirical adequacy but less simplicity.
Two types of coexistence were described earlier: when each competing theory (proposing natural selection or isolation) describes a causal factor, or when each theory-based model (Valence Bond or Molecular Orbital) provides
a useful perspective. A third type of coexistence, described in the paragraph
above, is when sub-theories that are in competition (because they describe the
same type of phenomena) “split up” the domain claimed by a mega-theory
that contains both sub-theories as components; each sub-theory has its own sub-domain
(consisting of those systems in which the sub-theory is valid) within the larger
domain of the mega-theory.
Newtonian Physics is another theory whose
initially wide domain (every system in the universe!) has been narrowed.
This change occurred in two phases. In 1905 the theory of Special (which Einstein wanted to call his theory of Invariance) declared that Newton's theory is not valid for objects moving at high speed.
And in 1925, quantum mechanics declared that it is not valid for objects with
small mass, such as electrons. Each of these new theories could derive
Newtonian Physics as a special case; within the domain where Newtonian Physics
was approximately valid, its predictions were duplicated by special relativity
(for slow objects) and by quantum mechanics (for high-mass objects). But
the reverse was not true; special relativity and quantum mechanics could not
be derived from Newton's theories, which made incorrect predictions for fast
objects and low-mass objects.
Even though quantum mechanics is currently considered valid for all systems, it is self-limited in an interesting way. For some questions the theory's answer is that “I refuse to answer the question” or “the answer cannot be known.” But a response of “no comment” is better than answers that are confidently clear yet wrong, such as those offered by the earlier Bohr Model. Some of the non-answers offered by quantum mechanics imply that there are limits to human knowledge. This may be frustrating to some people, but if that is the way nature is, then it is better for scientists to admit this (in their theories) and to say “sorry, we don't know that and we probably never will.”
3. Cultural-Personal Factors in Theory Evaluation
An Overview of Scientific Method, Section 3
THE JOY OF SCIENCE. For most scientists, a powerful psychological motivation is curiosity about "how things work" and a taste for intellectual stimulation. The joy of scientific discovery is captured in the following excerpts from letters between two scientists involved in the development of quantum mechanics: Max Planck (who opened the quantum era in 1900) and Erwin Schrodinger (who formulated a successful quantum theory in 1926).OTHER PSYCHOLOGICAL MOTIVES and PRACTICAL CONCERNS.
Most scientists try to achieve personal satisfaction and professional success
by forming intellectual alliances with colleagues and by seeking respect and
rewards, status and power in the form of publications, grant money, employment,
promotions, and honors.
When a theory (or a request for research
funding) is evaluated, most scientists will be influenced by the common-sense
question, "How will the result of this evaluation affect my own personal
and professional life?" Maybe a scientist has publicly taken sides
on an issue and there is ego involvement with a competitive desire to "win
the debate"; or time and money has been invested in a theory or research
project, and there will be higher payoffs, both practical and psychological,
if there is a favorable evaluation by the scientific community. In these
situations, when there is a substantial investment of personal resources, many
scientists will try to use logic and "authority" to influence the
process and result of evaluation.
METAPHYSICAL WORLDVIEWS. Metaphysics
forms a foundation for some conceptual factors, such as criteria for the types
of entities and interactions that should be used in theories. One example,
described earlier, was the preference by many astronomers, including Copernicus,
for using only circular motions at constant speed in their
theories.
Metaphysics can also influence logical structure.
Darden (1991) suggests that a metaphysical worldview in which nature is simple
and unified may lead to a preference for scientific theories that are simple
and unified.
A common metaphysical assumption in science
is empirical consistency, with reproducible results -- there is an expectation
that identical experimental systems should always produce the same observations.
(with "the same" interpreted statistically, not literally)
Metaphysical worldviews can be nonreligious,
or based on religious principles that are theistic, nontheistic, or atheistic.
Everyone has a worldview, which does not cease to exist if it is ignored or
denied. For example, to the extent that positivists
(also called empiricists) who try to prohibit unobservables in theories are
motivated by a futile effort to produce a science without metaphysics, they
are motivated by their own metaphysical worldviews.
IDEOLOGICAL PRINCIPLES are based on subjective values
and on political goals for "the way things should be" in society.
These principles span a wide range of concerns, including socioeconomic structures,
race relations, gender issues, social philosophies and customs, religions, morality,
equality, freedom, and justice.
A dramatic example of political influence
is the control of Russian biology, from the 1930s into the 1960s, by the "ideologically
correct" theories and research programs of Lysenko, supported by the power
of the Soviet government.
OPINIONS OF "AUTHORITIES" can also influence evaluation. The quotation marks are a reminder that a perception of authority is in the eye of the beholder. Perceived authority can be due to an acknowledgment of expertise, a response to a dominant personality, and/or involvement in a power relationship. Authority that is based at least partly on power occurs in scientists' relationships with employers, tenure committees, cliques of colleagues, professional organizations, journal editors and referees, publishers, grant reviewers, and politicians who vote on funding for science.
SOCIAL-INSTITUTIONAL CONTEXTS. These
five factors (psychology, practicality, metaphysics, ideology, authority) interact
with each other, and they develop and operate in a complex social context at
many levels — in the lives of individuals, in the scientific community, and
in society as a whole. In an attempt to describe this complexity, the
analysis-and-synthesis framework of ISM includes: the characteristics
of individuals and their interactions with each
other and with a variety of groups (familial, recreational,
professional, political,...); profession-related
politics (occurring primarily within the scientific community) and societal
politics (involving broader issues in society); and the institutional
structures of science and society.
The term "cultural-personal" implies
that both cultural and personal levels are important. These levels are
intimately connected by mutual interactions because individuals (with their
motivations, concerns, worldviews, and principles) work and think in the context
of a culture, and this culture (including its institutional structure, operations,
and politics, and its shared concepts and habits of thinking) is constructed
by and composed of individual persons.
Cultural-personal factors are influenced
by the social and institutional context that constitutes the reward system of
a scientific community. In fact, in many ways this context can be considered
a causal mechanism that is partially responsible for producing the factors.
For example, a desire for respect and approval is intrinsic in humans, existing independently
of a particular social structure, but the situations that stimulate this desire
(and the responses that are motivated by these situations) do depend on the
social structure. An important aspect of a social-institutional structure
is its effects on the ways in which authority is created and manifested, especially
when power relationships are involved.
What are the results of mutual interactions between science and society? How does science affect culture, and how does culture affect science?
SCIENCE AFFECTS CULTURE. The most obvious effect of science has been its medical and technological applications, with the accompanying effects on health care, lifestyles, and social structures. But science also influences culture, in many modern societies, by playing a major role in shaping cultural worldviews, concepts, and thinking patterns. Sometimes this occurs by the gradual, unorchestrated diffusion of ideas from science into the culture. At other times, however, there is a conscious effort, by scientists or nonscientists, to use "the authority of science" for rhetorical purposes, to claim that scientific theories and evidence support a particular belief system or political program.
CULTURE AFFECTS SCIENCE. ISM, which is mainly concerned with the operation of science, asks "How does culture affect science?" Some influence occurs as a result of manipulating the "science affects culture" influence described above. If society wants to obtain certain types of science-based medical or technological applications, this will influence the types of scientific research that society supports with its resources. And if scientists (or their financial supporters) have already accepted some cultural concepts, such as metaphysical and/or ideological theories, they will tend to prefer (and support) scientific theories that agree with these cultural-personal theories. In the ISM diagram this influence appears as a conceptual factor, external relationships...with cultural-personal theories. For example, the Soviet government supported the science of Lysenko because his theories and research supported the principles of Marxism. They also hoped that this science would increase their own political power, so their support of Lysenko contained a strong element of self-interest.
PERSONAL CONSISTENCY. Some cultural-personal
influence occurs due to a desire for personal consistency in life. According
to the theory of cognitive dissonance (Festinger,
1956), if there is a conflict between ideas, between actions, or between thoughts
and actions, this inconsistency produces an unpleasant dissonance, and a person
will be motivated to take action aimed at reducing the dissonance. In
the overall context of a scientist's life, which includes science and much more,
a scientist will seek consistency between the science and non-science aspects
of life. { Laudan has proposed a model for dissonance-driven "reticulated" change in science. }
Because groups are formed by people, the
principles of personal consistency can be extrapolated (with appropriate modifications,
and with caution) beyond individuals to other levels of social structure, to
groups that are small or large, including societies and governments. For
example, during the period when the research program of Lysenko dominated Russian
biology, the Soviets wanted consistency between their ideological beliefs and
scientific beliefs. A consistency between ideology and science will reduce
psychological dissonance, and it is also logically preferable. If a Marxist
theory and a scientific theory are both true, these theories should agree with
each other. If the theories of Marx are believed to be true, there tends
to be a decrease in logical status for all theories that are inconsistent with
Marx, and an increase in status for theories consistent with Marx. This
logical principle, applied to psychology, forms the foundation for theories
of cognitive dissonance, which therefore also predict an increase in the status
of Lysenko's science in the context of Soviet politics.
Usually scientists (and others) want theories
to be not just plausible, but also useful. With Lysenko's biology, the
Soviets hoped that attaining consistency between science policy and the principles
of communism would produce increased problem-solving utility. Part of
this hope was that Lysenko's theories, applied to agricultural policy, would
increase the Russian food supply; but nature did not cooperate with the false
theories, so this policy resulted in decreased productivity. Another assumption
was that the Soviet political policies would gain popular support if there was
a belief that this policy was based on (and was consistent with) reliable scientific
principles. And if science "plays a major role in shaping cultural...thinking
patterns," the government wanted to insure that a shaping-of-ideas by science
would support their ideological principles and political policies. The
government officials also wanted to maintain and increase their own power, so
self-interest was another motivating factor.
FEEDBACK. In the ISM diagram, three large arrows point toward "evaluation of theory" from the three evaluation factors, and three small arrows point back the other way. These small arrows show the feedback that occurs when a conclusion about theory status already has been reached based on some factors and, to minimize cognitive dissonance, there is a tendency to interpret other factors in a way that will support this conclusion. Therefore, each evaluation criterion is affected by feedback from the current status of the theory and from the other two criteria.
THOUGHT STYLES. In the case of Lysenko there was an obvious, consciously planned interference with the operation of science. But cultural influence is usually not so obvious. A more subtle influence is exerted by the assumed ideas and values of a culture (especially the culture of a scientific community) because these assumptions, along with explicitly formulated ideas and values, form a foundation for the way scientists think when they generate and evaluate theories, and plan their research programs. The influence of these foundational ideas and values, on the process and content of science, is summarized at the top of the ISM diagram: "Scientific activities...are affected by culturally influenced thought styles." Section 8 discusses thought styles: their characteristics; their effects on the process and content of science; and their variations across different fields, and changes with time.
OVER-GENERALIZING. When scholars are thinking about cultural-personal factors and their influence in science, too often there is too much over-generalizing. It's easy to get carried away into silly ideas, unless we remember that all of these cultural-personal factors vary in different areas of science and in communities within each area, and for different individuals, so the types and amounts of resulting influences (on the process of science and the content of science) vary widely.
CONTROVERSY. Among scholars who study science there is a wide range of views about the extent to which cultural factors influence the process and content of science. These debates, and the role of cultural factors in ISM and in science education, are discussed on the "Hot Debates about Science" page, especially in Part 3: Logic & Culture, Strong Criticisms, Two Analytical Tools, A Million Dollar Wager. Briefly summarized, my opinion is that an extreme emphasis on cultural influence is neither accurate nor educationally beneficial, and that even though there is a significant cultural influence on the process of science, usually (but not always) the content of science is not strongly affected by cultural factors.
4. Theory Evaluation
This is a relatively short section because
I don't want to duplicate the many discussions of evaluation in Sections 1-3
(three types of evaluative inputs), 5 and 6 (using evaluation to generate theories
and experiments), 7 and 8 (evaluation in research and thought styles), and 9
(critical thinking). And the EKS-RATED page discusses many controversial
ideas related to theory evaluation.
The overview briefly
describes the main concepts of evaluation: inputs from three types of
factors (empirical, conceptual, and cultural-personal), and an output of status
that is an estimate of a theory's plausibility
and/or usefulness; decisions to retain,
revise, or reject;
pursuit and acceptance;
rationally justified confidence instead of proof
or disproof; intrinsic status and relative
status.
This section will not review these concepts,
but will discuss (in more detail than elsewhere) four topics: delayed decision,
intrinsic and relative status, variable-strength conclusions and hypotheses,
and conflicts between different evaluative criteria.
DELAY. A fourth option for a decision
(in addition to retain, revise, and reject) is not shown in the ISM diagram:
there can be a delay in responding, while other
activities are being pursued. Sometimes there is no conscious effort to
reach a conclusion because there is no need to decide. However, a decision
(and action) may be required even though evaluation indicates that only a conclusion
of "inconclusive" is warranted. In this uncomfortable situation,
a wise approach is to make the decision (and do the action) in a way that takes
into account the uncertainties about whether or not the theory is true.
If a conclusion is delayed and a theory is
temporarily ignored while other options are pursued, and this theory is eventually
revived for pursuit or acceptance, then in hindsight we can either say that
during the delay the theory was being retained (with no application or development)
or that it was being tentatively rejected with the option of possible reversal
in the future. But if this theory is never revived, then when it was ignored
it was actually being rejected.
INTRINSIC STATUS and RELATIVE STATUS.
A theory has its own intrinsic status that is an estimate of the theory's plausibility
and/or usefulness. And if science is viewed as a search for the best theory
— whether "the best" is defined as the most plausible or the most
useful — there is implied competition, so each theory also has a relative status.
A change in the intrinsic status of one theory
will affect the relative status of competitive theories. In the ISM-diagram
this feedback is indicated by a small arrow pointing from "alternative
theories" to "status of theory relative to competitors."
A theory can have low intrinsic status even
if it is judged to be better than its competitors and therefore has high relative
status, if evaluation indicates that none of the current theories is likely
to be true or useful. For example, before publication of the famous double
helix paper in April 1953, an honest scientist would admit that "we don't
know the structure of DNA." After the paper, however, among knowledgeable
scientists this skepticism quickly changed to a confident claim that "the
correct structure is a double helix." In 1953 the double helix theory
attained high intrinsic status and relative status, but before 1953 all theories
about DNA structure had low intrinsic status, even though the best of these
would, by default, have high relative status as "the best of the bad theories."
VARIABLE-STRENGTH CONCLUSIONS and HYPOTHESES.
In ISM the concept of "status" (Hewson, 1981) is a reminder that the
conclusion of theory evaluation is an educated estimate rather than certainty.
This concept is useful because it allows a flexibility that doesn't force thinking
into dichotomous yes-or-no channels.
Another stimulater of flexible, careful thinking
is ISM's definition (based on Giere, 1991) of a hypothesis
as a claim that a system and a theory-based model are similar in specified respects
and to a specified (or implied) degree of accuracy. With this definition,
different hypotheses can be framed for the same model. The strongest hypothesis
would claim an exact correspondence between all model-components and system-components,
while a weaker hypothesis might claim only an approximate correspondence, or
a correspondence (exact or approximate) for some components but not for all.
If a theory is judged to be only moderately plausible, the uncompromising claims
of a strong hypothesis will be rejected, even though scientists might accept
the diluted claims of a weak hypothesis.
CONFLICTS BETWEEN CRITERIA. Some of
the tensions between different types of evaluation criteria are briefly outlined
in this sub-section. { Each conflict is discussed in more detail
elsewhere. }
An estimate of predictive
contrast requires a consideration of how likely it is that "plausible
alternative theories" might make the same predictions. The word "plausible"
indicates that empirical adequacy (by making correct predictions) is not the
only relevant constraint on theory generation. To illustrate, Sober (1991,
p. 31) tells a story about explaining an observation (of "a strange rumbling
sound in the attic") with a theory ("gremlins bowling in the attic")
that is empirically adequate yet conceptually implausible.
When a theory is simplified
(which is usually considered a desirable conceptual factor) the accuracy of
its predictions may decrease (which is undesirable according to empirical criteria).
In this situation there may also be conflicts between the conceptual criteria
that a theory should be complete (by including all essential components) and
simple (with no extraneous components), because usually there is inherent tension
between completeness and simplicity.
There can also be conflict between explanatory
adequacy and the positivist claim that a theory should not
try to explain observations by postulating unobservable entities, actions or
interactions.
There are varying degrees of preference in
different fields (and by different scientists) for unified
theories with wide scope, relative to other criteria.
Interaction between empirical factors occurs
when there is data from several sources. Scientists
want a theory to agree with all known data, but to obtain agreement with one
data source it may be necessary to sacrifice empirical adequacy with respect
to another source.
And there can be conflict between cultural-personal
factors and other factors, as discussed in Section 3.
5. Theory Generation
An Overview of Scientific Method, Section 5
This section builds on the foundation of Theories and Supplementary Theories in Section 1.
SELECTION AND INVENTION. Scientists can generate a theory by selecting an old theory or — if there is some dissatisfaction with old theories, or if a curious scientist just wants to explore other possibilities — by inventing a new theory. { As defined in ISM, the revision of an existing theory is invention, and the revised theory is called a "new theory" even though it is not totally new. Invention thus includes the small-scale incremental theory development that is common in science, not just the major conceptual revolutions that, although important, are rare. } In the following discussion the process of "selection and/or invention" will usually be called "generation" or "proposal".
The rest of this section describes strategies for selecting or inventing theories.
RETRODUCTION and DEDUCTION. In contrast
with deductive logic that asks, "If this is the model, then what will the
observations be?", retroductive logic — which uses deduction supplemented
by imaginative creativity — asks a reversed question in the past tense, "These
were the observations, so what could the model (and theory) have been?"
The essence of retroductive inference is doing thought-experiments, over and
over, each time "trying out" a different model that is being proposed
(by selection or invention) with the goal of producing predictions
(i.e. theory-based deductions) that match the known observations. Basically, the goal is to find a theory
that, if true, would explain what has been observed.
Retroduction is useful when, after an experiment
is over, scientists are not sure that they know how to interpret what happened.
In this context of uncertainty they search for a theory (either old or new)
that will help them make sense of what they have observed. Strategies for retroductive generation of theories are described below.
RETRODUCTION and HYPOTHETICO-DEDUCTION are logically identical except for timing; in retroduction a theory is proposed after observations are known. Both try to answer the same question — Is the model similar to the system? — by comparing predictions with observations in order to estimate degrees of agreement and predictive contrast. Both types of logic can be used as inputs for "empirical evaluation of current hypothesis." And both are limited to an "if... then maybe..." uncertain conclusion, in contrast with the "if... then..." certain conclusion of deductive logic. Even though prediction implies that the deduction is made before observations are known, it doesn't make any logical difference if the theory-based deduction (= prediction) is made before or after observations are known, IF the deductive logic is valid. But the "IF" is important because, compared with hypothetico-deduction, with retroduction there should be more concern about the possibility of using ad hoc adjustments to achieve a match between predictions and known observations. This concern applies to retro-selection, and even more to retro-invention. The possibility of ad hoc adjustment is important when we're thinking about a theory's logical systematicity and simplicity, as in applying Occam's Razor.
DOMAIN-THEORIES and SYSTEM-THEORIES.
A theory-based model of an experimental
system is constructed from two sources: a general domain-theory
(about the characteristics of all systems in a domain) and a specific system-theory
(about the characteristics of one experimental system). During retroduction,
either or both of these theories can be revised in an effort to construct a
model whose predictions will match the known observations.
But a system-theory and domain-theory are
not independent. While playing with the possibilities for revising these
theories, an inventor may discover relationships between them. In particular,
a domain-theory (about all systems in the theory's domain) will usually influence
a system-theory about one system in this domain.
An interesting example
of revising a specific system-theory was the postulation of Neptune. In the mid-1800s,
data from planetary motions did not precisely match the predictions of a general domain-theory, Newtonian Physics. By assuming the domain-theory was valid, scientists
retroductively calculated that if the system contained an extra planet, with
a specified mass and location, predictions would match observations. Motivated
by this newly invented system-theory with an extra planet, astronomers searched
in the specified location and discovered Neptune. Later, in an effort
to resolve the anomalous motion of Mercury, scientists tried this same strategy
by postulating an extra planet, Vulcan, between Mercury and the Sun. But
this time there was no extra planet; instead, the domain-theory (Newtonian physics)
was at fault, and eventually a new domain-theory (Einstein's theory of general
relativity) made correct predictions for the motion of Mercury. In each
example, one of the components used for constructing a model were revised; there was a change in the system-theory (with Neptune) and in the domain-theory (for Mercury).
In another example, described earlier, the discovery of radioactivity in 1903 caused a revision
of a system-theory for the earth's interior geology. This revised system-theory,
combined with observations (of the earth's temperature) and a domain-theory
(thermodynamics), required a revision in another theory component (the earth's
age), thereby settling an interfield conflict that began in 1868, between geologists (who said "the earth is old") and physics who said "the earth cannot be old" because (without the extra source of heat-energy that was unknown before 1903) the earth would now be cooler than we observe.
What are the results of theory generation?
In the ISM-diagram, arrows point from theory generation to system-theory and
domain-theory, because both are needed to construct a model. Three more
arrows point to "theory" and "supplementary theory" (because
both can be used for constructing a domain-theory) and to "alternative
theory" because a newly invented theory competes with the original unrevised
theory. Or the original theory might become an alternative, since labeling
depends on context; what scientists consider a main theory in one situation
could be alternative or supplementary in other situations.
RETRODUCTIVE GENERALIZATION.
If there is data from several experimental systems, the empirical constraints
on retroduction can be made more rigorous by demanding that a theory's predictions
must be consistent with all known data. This process of retroductive
generalization generates a theory whose domain includes all the systems.
In fact, the domain is usually larger than all of the systems combined, because
the domain-theory is assumed to be valid for a whole class of systems; this
class extends beyond (and contains as a subset) the systems for which there
is available data.
A generalization also occurs when an existing
theory is selected for application to a system that was not within the domain
previously claimed for the theory.
A summary: Retroductive generalization
converts many models (each for one system) into a general theory (for many systems),
or it widens the domain of an existing theory. But in deduction (which
is used during retroduction or hypothetico-deduction) a general theory is applied
to construct a specific model for one system.
STRATEGIES FOR RETRO-GENERALIZING.
When retroduction is constrained by multiple sources of data, it may be easier
to "cope with the complexity" if a simplifying strategy is used.
Instead of trying to think about all the systems at once, first infer a model
for one system, and then apply "the principles for this model" (i.e.,
a theory from which the model could be derived) to construct models for the
other systems, to test whether this theory can be generalized to fit all the
known data.
A more holistic strategy is to creatively
search the data looking for an empirical pattern that, once recognized, can
provide the inspiration and guiding constraints for inventing a composition-and-operation
mechanism that explains the pattern. This process begins with no theory;
then there is a descriptive theory (based on an
empirical pattern) that can be converted into an
explanatory theory. While searching for patterns,
a scientist can try to imagine new ways to see the data and interpret its meaning.
Logical strategies for thinking about multiple experiments, such as Mill's Methods
of inquiry, can be useful for pattern recognition and theory generation.
RETRODUCTION and INDUCTION. Most of the discussion above has focused on the use of deductive logic during retroduction. Usually, however, retroduction also involves some inductive logic. At this time I won't try to separate (or to interrelate) the typical functions and contributions of deduction and induction. But the eclectic nature of generative inference should be recognized: usually, a scientific "inference to the best explanation" involves a creative blending of logic that is both inductive and deductive. top of page
GENERATION AND EVALUATION. Although
C.S. Peirce (in the 1800s) and Aristotle (much earlier) studied theory invention,
as have many psychologists, most philosophers separated evaluation from invention,
and focused their attention on evaluation. Recently, however, many philosophers
(such as Hanson, 1958; and Darden, 1991) have begun to explore the process of
invention and the relationships between invention and evaluation. Haig
(1987) includes the process of invention in his model for a "hypothetico-retroductive
inferential" scientific method.
Generation (by selection or invention) and
evaluation are both used in retroduction, with empirical evaluation acting as
a motivation and guide for generation, and generation producing the idea being
evaluated. It is impossible to say where one process ends and the other
begins, or which comes first, as in the classic chicken-and-egg puzzle.
The generation of theories is subject to
all types of evaluative constraints. Empirical adequacy is important,
but scientists also check for adequacy with respect to cultural-personal factors
and conceptual criteria: internal consistency, logical structure, and external
relationships with other theories.
INVENTION BY REVISION. Invention often begins with the selection of an old (i.e., previously existing) theory that can be revised to form a new theory.
ANALYSIS AND REVISION. One strategy
for revising theories begins with analysis; split a theory into components and
play with them by thinking about what might happen if components (for composition
or operation) are modified, added or eliminated, or are reorganized to form
a new structural pattern with new interactions.
According to Lakatos (1970), scientists often
assume that a "hard core" of essential
theory components should not be changed, so an inventor can focus on
the "protective belt" of auxiliary
components that are devised and revised to protect the hard core.
Usually this narrowing of focus is productive, especially in the short term.
But occasionally it is useful to revise some hard-core components. When
searching for new ideas it may be helpful to carefully examine each component,
even in the hard core, and to consider all possibilities for revision, unrestrained
by assumptions about the need to protect some components. By relaxing
mental blocks about "the way things must be" it may become easier
to see theory components or data patterns in a new way, to imagine new possibilities.
Or it may be productive to combine this analytical
perspective with a more holistic view of the theory, or to shift the mode of
thinking from analytical to holistic.
INTERNAL CONSISTENCY. Another invention
strategy is to construct a theory, using the logic of internal consistency,
by building on the foundation of a few assumed axiomatic components.
In mathematics, an obvious example is
Euclid's geometry. An example from science is Einstein's theory of
Special Relativity; after postulating that two things are constant
(physical laws in uniformly moving
reference frames, and the observed speed of light), logical consistency —
which Einstein explored with mental experiments — makes it necessary that
some properties
(length, time, velocity, mass,...) will be relative while other properties
(proper time, rest mass,...) are constant. A similar strategy was
used in the subsequent invention of General Relativity when, with the help
of a friend (Marcel
Grossmann) who was an expert mathematician, Einstein combined his empirically
based physical intuitions with the powerful mathematical techniques of multidimensional
non-Euclidean geometry and tensor calculus that had been developed in the
1800s.
Although empirical factors played a role
in Einstein's selection of initial axioms, once these were fixed each theory
was developed using logical consistency. Responding to an empirical verification
of General Relativity's predictions about the bending of light rays by gravity,
even though Einstein was elated he expressed confidence in his conceptual criteria,
saying that the empirical support did not surprise him because his theory was
"too beautiful to be false."
EXTERNAL RELATIONSHIPS. Sometimes new
ideas are inspired by studying the components and logical structure of other
theories. Maybe a component can be borrowed from another theory; in this
way, shared components become generalized into a wider domain, and systematic
unifying connections between theories are established.
Or some of the structure in an old theory
can be retained (with appropriate modification) while the content of the old
components is changed, thereby using analogy to guide the logical structuring
of the new theory.
Another possibility is mutual analysis-and-synthesis;
by carefully comparing the components of two theories, it may be possible to
gain a deeper understanding of how the two are related by an overlapping of
components or structures. This improved understanding might inspire a
revision of either theory (with or without borrowing or analogizing from the
other theory), or a synthesis that combines ideas from both theories into a
unified theory that is more conceptually coherent and has a wider empirical
scope.
And sometimes a knowledge of theories in
other areas will lead to the recognition that an existing theory from another
domain can be generalized, as-is or modified, into the domain being studied
by a scientist. This is selection rather than invention, but it still
"brings something new" to theorizing in the domain. And the
process of selection is similar to the process of invention, both logically
and psychologically, if (as in this case) selection requires the flexible, open-minded
perception of a connection between domains that previously were not seen as
connected.
6. Experimental Design (Generation-and-Evaluation)
An Overview of Scientific Method, Section 6
When scientists generate and evaluate experiments (i.e., when they design experiments), they consider the current state of theory evaluation; they check for gaps in their knowledge of systems; and they do thought-experiments for a variety of potential experimental systems, looking for systems that might produce useful results.
FIELD STUDIES. In my model for Integrated Scientific Method an "experiment" includes both highly controlled experiments and minimally controlled field studies. In a field study a scientist has little or no control over the naturally occurring phenomenon being studied (such as wildlife ecology, starlight, dinosaur fossils, or an earthquake), although there is some control over how to collect observation-data — where to go and what to observe in a wildlife setting, how to observe starlight, where to dig for fossils, or what type of seismographic equipment to use & where to place it, and what kinds of post-quake followups to do — and how to analyze the data. Sometimes, additional observations (and controlled experiments on collected artifacts) can be done.
GOAL-DIRECTED DESIGN. Sometimes experiments are done just to see what will happen, to gather observations for an empirical database that can be interpreted in the future. Often, however, experiments are designed to accomplish a goal. The next five subsections (with *s) examine some ways in which the pursuit of scientific goals can motivate and guide the design of experiments.
* LEARNING ABOUT SYSTEMS AND THEORIES.
Theory evaluation can provide essential
input for experimental design, by revealing four types of "trouble spots"
to investigate by experimentation. If there is anomaly, maybe an experiment
can localize its source, or test options for theory revision. If there
is a lack of support for (or against) a theory, a well designed experiment may
provide more evidence. If there is low predictive contrast, scientists
can try to design a "crucial experiment" that discriminates between
the competitive theories. And if there is conceptual difficulty, this
can inspire an experiment to learn more about the problematic aspect of the
theory.
Or scientists can be motivated by domain evaluation.
When they examine their empirical knowledge of a domain, they may find a
gap in system knowledge that reveals an opportunity
for learning. Thus, when scientists design an experiment they can be mainly
interested in learning about either a theory or an experimental system.
For either type of goal,
interpretive logic is available. For a particular experimental system,
if scientists assume they know the system-theory, they can
make inferences (either hypothetico-deductive or retroductive) about a domain-theory.
But if they assume the domain-theory is
known, their inferences are about a system-theory.
This principle, that inference can involve
a domain-theory or system-theory, is useful for designing experiments with different
goals. For example, scientists may assume they know a domain-theory about
one property of a chemical system, and based on this knowledge they design a
series of experiments for the purpose of developing system-theories that characterize
this property for a series of chemical systems. But the goal changes when
scientists use a familiar chemical system and assume they have an accurate system-theory
(about a number of chemical properties that are well characterized due to the
application of existing domain-theories) in order to design an experiment that
will let them develop a new domain-theory about another chemical property.
Often, however, both types of knowledge increase
during experimentation. Consider a situation where scientists assume a
domain-theory about physiology, and use this theory to design a series of experiments
with different species, in order to learn more about each species. While
they are learning about these systems, they may also learn about the domain-theory:
perhaps it needs to be revised for some species or for all species; or
they may persuade themselves about the truth of a claim (that the same theory
can be generalized to fit all the species being studied) that previously had
been only an assumption.
Sometimes, in the early stages of developing
a theory in an underexplored domain, scientists can assume neither a system-theory
nor a domain-theory; their knowledge gap is both empirical and theoretical,
with very little data about systems, and no satisfactory theory. An example
of dually inadequate knowledge occurred in the early 1800s when atomic theory
was being developed, and chemists were also uncertain about the nature of their
experimental systems, such as whether in the electrolysis experiment of "water
--> hydrogen + oxygen" the hydrogen was H or HH, the oxygen was O or
OO, and the water was HO or HOO or HHO.
* LEARNING ABOUT EXPERIMENTAL TECHNIQUES is another
possible goal. For example, x-ray diffraction can now be used to help
determine the structure of molecules. But in the early days of xray experiments
the major goal was to learn more about the technique by studying variables such
as xray wavelength, width and intensity of beam, angle of incidence, sample
preparation and thickness, and type of detector. This knowledge was then
used to design theories about the correlations between x-ray observations and
molecular structure.
In pursuing knowledge about a new technique,
a powerful strategy is to design controlled cross-checking
experiments in which the same system is probed with a known technique
and a new technique, thus generating two data sets that can be compared in order
to "calibrate" the new technique.
For example, if a familiar technique records numerical data of "40.0, 50.0,
60.0, 70.0, 80.0" for five states of a system, and a new technique measures
these states as "54.4, 61.2, 67.1, 72.2, 76.8" we can infer that a
"new 54.4" corresponds to an "old 40.0," and so on.
A similar strategy can be used for qualitative
calibration. For example, if we somehow know that four solutions contain
ions of Li, Na, K and Cs, we can observe the color produced when a wire is dipped
into each solution and placed in a flame. Based on this descriptive domain-theory
for these applications of the flame technique, we can then remove the labels
from the bottles, test each solution in a flame, and infer system-theories about
the contents of each bottle. This strategy, in a more sophisticated form
but using similar logic, was employed by Watson and Crick in 1953 when x-ray
observations helped them retroductively infer a structure for DNA.
* ANOMALY RESOLUTION. If predictions
and observations do not agree, two possible causes are an inadequate system-theory
or domain-theory. In either case, maybe a new experiment can localize
the anomaly to a faulty theory-component, and further experiments can test options
for revising this component.
A third possible cause of anomaly is misleading
observations. For example, in an experimental system that includes a voltage
meter, an inaccurate meter might read 4.1 Volts when the actual voltage is 5.7
Volts. If the observation of 4.1 Volts is assumed to be accurate, scientists
may try to revise a domain-theory or system-theory even though "it doesn't
need fixing." But if there are good reasons to believe the model
is accurate, scientists can do a troubleshooting
analysis — similar to the logic used by an automechanic (or physician) trying
to determine what has gone wrong with an engine (or body) — in an effort to
find the cause of anomaly. After the faulty meter is discovered and the
system-theory is revised to include "a meter that reads 28% low,"
predictions will match observations. Or the faulty meter can be replaced
by a meter that produces accurate observations.
Another type of anomaly occurs when scientists
are surprised, not by a disagreement between observations and predictions, but
by a difference between observations and previous observations in similar (or
apparently identical) experiments. The surprise arises due to a metaphysically
based assumption of reproducibility, an expectation that the same system should
always produce the same results. (of course, "the same"
must often be interpreted statistically)
Or maybe what actually happened is more interesting
than what was planned, as in the unexpected occurrence of penicillin or Teflon,
and the anomaly is an opportunity for serendipitous discovery that will result
in a publication, a patent, or even a Nobel Prize.
* CRUCIAL EXPERIMENTS. Sometimes instead
of anomaly there is agreement, but with too many theories. In this situation
a sensible strategy is to design a more discriminating "crucial experiment"
whose outcome will lend clear support to one competitor or the other.
When designing for this goal, an effective strategy is to run thought-experiments
(for all competitive theories, for a variety of potential experimental systems)
and check for predictive contrast.
For example, to test an Olympic
Weightlifter Theory, asking John to lift 10 pounds or 1000 pounds will be
useless, but asking him to lift an intermediate weight (an amount that could
be lifted by an OW but not by others) would provide useful information.
Or consider a liquid that conducts electricity
well. One explanation is that the liquid contains NaCl in water.
This system-theory produces a high degree of agreement — because domain-theories
(involving NaCl, water, dissolving, ions, and conductivity) predict that aqueous
NaCl will conduct electricity — but this retroductive inference is uncertain
due to low predictive contrast, because many other system-theories (such as
water with HCl, NaOH, or KBr; or NaCl in methanol) also predict high conductivity.
In an effort to eliminate alternative theories, a scientist could design other
experiments, such as testing for acidity or basicity (to test for HCl or NaOH),
observing the flame color (for Na or K), determining the density, flammability
or odor (for methanol), and so on. These experiments could support the
NaCl/water theory or weaken it, but could not prove it true. In this example
the scientist assumes the adequacy of domain-theories (involving ions,...) in
order to evaluate the status of alternative system-theories. But in other
situations the status of one or more domain-theories might be the focus of evaluation.
* HEURISTIC EXPERIMENTS and DEMONSTRATIVE EXPERIMENTS
differ in their objectives (Grinnell, 1992). Early in their explorations,
to learn more about a domain or theory, scientists design heuristic
experiments. Later, the goal can shift toward the design of impressive
demonstrative experiments that will be useful for
persuading others about a domain-theory or system-theory by clearly highlighting
its strengths or weaknesses.
For either type of experiment, but especially
for demonstration, a useful strategy is to think ahead to questions that will
be raised during evaluation. These questions — about sample size and
representativeness, systematic errors and random errors, adequacy of controls
for all relevant factors, predictive contrast, and so on — can be used to probe
the current empirical knowledge, searching for gaps that should be filled by
experimentation. When doing this it is wise to be brutally critical, at
least as tough as one's critics will be, by trying to imagine their toughest
questions and challenges, and answering them.
Often an informative heuristic experiment
will also be effective for demonstration. For example, a crucial experiment
that distinguishes between plausible alternatives is useful in any context.
But there can be significant differences in the motivation of scientists when
they design an experiment; are they mainly interested in learning or persuading?
For example, do they want to increase a sample size to address their own doubts,
or because this will be more persuasive in a paper they plan to publish?
And the two goals will often produce different experiments. For example,
do scientists run a novel experiment because they are curious about what will
happen, or a familiar experiment that has been refined to "clean up the
loose ends" so it becomes a more impressive demonstration of what is already
known?
A typical shift in experimental design, as
knowledge increases and motivations change, is that during an early heuristic
phase, knowledge may not provide much guidance, but in a later demonstration
phase there is enough knowledge (of theories and/or systems) that its guidance
can be more focused and precise.
LOGICAL STRATEGIES for experimental design.
To facilitate the collection and interpretation of data for any of the goals
described above, logical strategies are available. Scientists can use
hypothetico-deduction or retroduction to make inferences about
a domain-theory or system-theory. Or they can calibrate a new experimental
technique with cross-checking logic that compares data
from the new technique and a familiar technique.
Logical strategies — such as the systematic variation of parameters (individually or in
combinations) to establish "controls",
to discover correlations, and to determine the
individual or combined effects of various factors — can be useful for designing
clusters of experiments to generate data that is especially informative.
One such strategy is Mill's Methods for experimental inquiry. Complementary
"variations on a theme" experiments can be planned in advance, or
improvised in response to feedback from previous experimental results.
By using inductive logic, a descriptive or
explanatory theory can be generalized into an unexamined part of a domain.
In making the logical leap of generalizing observations (or principles) from
a small sample to a larger population, scientists depend on two main criteria:
statistical analysis (by considering sample size, degree of agreement,...) and
sampling accuracy (by asking whether the sample accurately represents the whole
population). These criteria can be used for controlled experiments or
field studies.
In addition to these types of logic, each
area of science has its own principles for designing experiments. In certain
types of medical or social science experiments, for example, there are usually
design features such as "blind" observation
and interpretation, or controls for psycho-physical placebo effects and for motivational
factors (Borg & Gall, 1989) such as the John Henry Effect, Pygmalion
Effect, and Hawthorne Effect.
VICARIOUS EXPERIMENTATION. So far, this
discussion has not challenged an implicit assumption that the only way to collect
observations is to do an experiment. But one scientist can interpret what
another observes, so a "theoretician" can vicariously design-and-do
experiments by reading (or hearing) about the work of others, in order to gather
observations for interpretation.
This strategy won a Nobel Prize for James
Watson and Francis Crick. They never did any productive DNA experiments,
but they did gather useful observations from other scientists: xray diffraction
photographs (from Rosalind Franklin), data about DNA's water content (also from
Franklin), data about the ratios of base pairs (from Erwin Chargaff), and information
about the chemistry and structure of DNA bases (from Jerry Donohue). Then
they interpreted this information using thought-experiments and physical models,
and they retroductively invented a theory for DNA structure. Even though
they did not design or do experiments, a similar function was performed by their
decisions about gathering (and paying close attention to) certain types of observations.
CUSTOMIZED DESIGN. Effective problem formulation is customized to fit the expertise and resources of a particular research group. For example, if members of one group are expert at theorizing about a certain molecule, they may use a wide variety of experimental techniques (plus reading and listening) to gather information about their molecule. Another group, whose members have the expertise (and the expensive machine) required to do a difficult experimental technique, may search for a wide variety of molecules they can study with their technique.
TAKING ADVANTAGE OF OPPORTUNITIES. Often,
new opportunities for scientific research emerge from a change in the status
quo. A newly invented theory can stimulate experiments with different
goals: to test the theory and, if necessary, revise it; to explore
its application for a variety of systems within (or beyond) its claimed domain;
or to calculate the value of physical constants in the theory.
New experimental systems can be produced
by new events (a volcanic eruption,...) or by newly discovered data (rocks on
Mars,...) or phenomena (such as radioactivity in 1896, or quasars in 1960).
New experiments can include field studies of natural phenomena, and controlled
experiments such as the labwork used to study dinosaur bones.
New instrumentation technologies or observation
techniques can produce opportunities for designing new types of experimental
systems. When this occurs a scientist's goal can be to learn more about
an existing theory or domain by using the new tool, or to learn more about the
tool. Scientists can design their own instruments, or they can use technology
developed mainly for other purposes, or they can provide motivation for developing
new technologies by making known their wishlist along with a promise that a
market will exist for the new products. Or old technologies can be used
in a new way, such as setting up the Hubble Telescope on a satellite above the
optically distorting atmosphere of the earth.
When an area opens up due to any of these changes, for awhile the possibilities for research are numerous. To creatively take advantage of a temporary window of opportunity, an open-minded awareness (to perceive the possibilities) and speed (to pursue possibilities before they vanish due to the work of others) are often essential. For example, Humphrey Davy used the newly developed technique of electrolysis to discover 7 elements in 1807 and 1808. Of course, in science (as in the rest of life) it helps to be lucky, to be in the right place at the right time, but to take advantage of opportunity a person must be prepared. As Louis Pasteur was fond of saying, "Chance favors the prepared mind." Many other scientists were working in the early 1800s, yet it was Davy who had the most success in using the new technique for discovery.
THOUGHT-EXPERIMENTS IN EXPERIMENTAL DESIGN. Mental
experiments — done to quickly explore a wide variety of experimental possibilities
ranging from conventional techniques to daring innovations — serve as a preliminary
screening process to decide which experimental systems are worthy of further
pursuit. Because thought-experiments are quick and cheap, compared with
physical experiments that typically require much larger investments of time
and money, they are an effective strategy for generating and evaluating ideas
for experiments.
Usually, mental experiments are a prelude
to physical experiments. But thought-experiments can be done for their
own sake, to probe the logical implications of a theory by deductively exploring
systems that may be difficult or impossible to attain physically. One
famous example is Einsteins's use of imaginary rockets & trains and activities (like riding on a photon) during
his development of relativity theory, so he could ask "what would happen if..."
FOUR CONTEXTS FOR THOUGHT-EXPERIMENTS.
Thought-experiments play a key role in three parts of ISM. In each context
a prediction is generated from a theory by using deductive logic, but there
are essential differences in objectives. In the process of experimental design the divergent objectives — looking
for experimental outcomes that might be interesting or useful — are less clearly defined
than during retroduction where,
despite a divergent search for theories, the convergent objective is to find a model
whose predictions match the known observations. And in
hypothetico-deduction, mental experiments are
even more constrained, being done with only one theory and one system.
In addition, thought-experiments can be used
for deductive exploration, by using a theory to
imagine what would happen in an exotic difficult-to-attain system. In
this context there are no physical constraints, so the only limits are those
imposed by the imagination. And the only cost is the time invested in
designing and running the mental experiments.
7. Goals and Actions in Problem Solving
As an introduction to this section, you should read Section 7 of the overview which provides a coherent overview of: problem formulation (by defining a now-state and a goal-state) and problem solving; scientific projects for improving our knowledge (which includes observations and interpretations); preparation and persuasion; and levels of problems (mega-problem, problem, sub-problems, actions) interacting with action evaluation.
PREPARATION. Before and during problem
formulation, scientists prepare by learning the current now-state of knowledge
about a selected area of nature, including theories, observations, and experimental
techniques. Early in the career of a scientist, as a student, typically
most preparation comes by reading books and listening to teachers, with supplementation
by first-hand experience in observation and interpretation. Later, when
a scientist is actively involved in research, typically there is a shift toward
an increased reliance on the learning that occurs during research, but some
learning still occurs by reading and listening. When a scientist becomes
more intellectually mature, less knowledge is accepted solely due to a trust
in authority, because there is an increase in the ability and willingness to
think critically.
As suggested by Perkins & Salomon (1988),
knowledge utilization can be viewed from two perspectives: backward-reaching and forward-reaching.
Scientists can reach backward in time, to use now what they have learned in
the past by reading, listening, and researching. Or they can focus on
learning from current experience, because they are looking forward to potential
uses of this knowledge in the future.
Because one scientist can interpret what
another observes, sometimes an effective strategy for collecting data is to
be a "theoretician" by reading (or hearing) about
the experiments of others, for the purpose of gathering observations that can
then be interpreted.
GOAL-CONSTRAINTS. Nickles (1981) provides an in-depth analysis of problem solving, and suggests that a problem is defined by specifying a set of constraints on its solution, which is done by specifying the characteristics of a goal-state (or a class of goal-states) that would be considered a satisfactory solution. Thinking of a goal-state in terms of "constraints" offers an interesting perspective.
SECONDARY GOALS. The primary goal of science is an improved knowledge about nature. But scientists are often motivated by cultural-personal factors such as satisfying their "psychological motives and practical concerns" by achieving concrete secondary goals: obtaining funds for research, getting a paper published,...
PRIMARY GOALS. Knowledge about nature includes both observations and interpretations. Although the ultimate goal of science is to produce theories (interpretations), immediate goals (such as funding and publications) often involve the design and execution of experiments to produce observations that can then be interpreted.
QUESTIONS, OBJECTIVES or PROBLEMS. Although ISM describes projects in terms of problem solving, scientists can define their goal as answering a question, achieving an objective, or solving a problem. Although there are subtle differences between these perspectives, they are basically equivalent.
PROJECT FORMULATION and DECISION.
The movement from problem to project requires evaluation and decision.
Members of a research group must evaluate the potential benefits of a proposed
project, compared with other alternatives, and ask the "so what" question
— "Why should we do this?" — in order to decide whether it is likely
to be a wise investment of their time and effort.
The ISM definition of a problem differs from
that of Nickles (1981, p. 109) who states that "a problem consists of all
the conditions or constraints on the solution plus the demand that the solution...be
found." Nickles' definition of a problem (constraints plus demand)
corresponds to my definition of a project. ISM and IDM distinguish between
problems and projects because this makes it easier to discuss the actual practice
of science and design, where problems can be formulated (or simply recognized)
even if their solution is not actively pursued. And I think the ISM-IDM
definition of a problem is more commonly used by people in a wide range of areas,
which makes it easier to discuss problems with straightforward simplicity, without
being misunderstood.
When deciding whether a problem solution
should be pursued, an important consideration is the existence of actions that
may lead to a solution. In other words, are there valid reasons for hope?
An effective problem formulation aims for a level of difficulty that is appropriate
— that is challenging (usually but not always this is necessary for achieving
significant results) yet is capable of being solved with the available resources
of time, people, knowledge, equipment, materials, and money.
Although it is possible to commit resources
and launch a project based on an assumption that a problem can be solved,
or a conviction that it must be solved, usually a decision to pursue
a project is preceded by some planning of specific actions. Because the
amounts of preliminary action-planning vary from one project to another, it
can be useful to define a project as either "a problem plus a decision
to pursue a solution," or as "a problem and a plan for solving it,
plus a decision to pursue this plan of action."
ACTION GENERATION-AND-EVALUATION. In
an effort to solve a problem, scientists invent, evaluate, and execute actions
that involve observation (design and do experiments
or field studies, make observations, or learn the observations of others) or
interpretation (organize data to facilitate pattern
recognition, analyze and synthesize, use algorithms and heuristics, select or
invent theories, evaluate theories, or review the interpretations of others).
Probing often involves recurring cycles of
observation-and-interpretation: interpretations (of previous observations) are
used to design experiments which produce observations that are used in further
interpretation, and the cycle begins again. During each cycle there can
be an increase in knowledge for both observations and interpretations, as well
as a preparation for future cycles.
Action generation-and-evaluation, whether
done to decide "what to do next" or to make long-term plans, is oriented
toward seeking a solution. An awareness of the current "state of the problem" serves as a guidance system
for the effective planning of actions. To develop and use this awareness,
the evaluator tries to understand the constantly changing now-state so this
can be compared with the goal-state (which is as an aiming point that orients
the search for a solution) in order to search for problem
gaps (specific ways in which the now-state and goal-state differ) that
can guide the planning of actions designed to close these gaps.
The process of action evaluation, which is
itself an action, is analogous to the process of theory evaluation. Of
course, evaluation must be preceded by another important action, the generation
(by selection or invention) of ideas for the potential actions that will be
evaluated.
CONCLUSION. The central step in action evaluation — comparing the current now-state with the goal-state — can be viewed as an evaluation of potential solutions. As the project continues, usually the now-state becomes increasingly similar to the goal-state. Eventually the now-state may be evaluated as satisfactorily similar, based on criteria defined by the problem constraints, and the problem is solved. Or at some point there may be a decision to abandon the project, at least temporarily, because progress toward a solution is slow, or because despite satisfactory progress the research group decides that working on another project is likely to be even more productive.
PERSUASION. The persuading can be internal
(within a research group, in discussions about how to execute or interpret
the research) or external. With external persuasion the goal might be
to convince others that observations made by the research group are accurate,
or that a proposed theory is worthy of acceptance (as plausible, useful knowledge)
or pursuit (to investigate by further research), that a paper should be published,
or
that a proposed project should be supported financially.
3Ps and 4Ps. A 3Ps
model of science (Peterson & Jungck, 1988) interprets scientific problem
solving in terms of posing, probing
and persuasion. A brief summary of the 3Ps
is that scientists pose a problem, then probe the problem in an effort to solve
it, and try to persuade themselves and others that their solution is satisfactory.
This simple model, which portrays the overall flow of research, was initially
proposed for the main purpose of influencing science education. In this
role it has stimulated a great deal of productive thinking about science and
science education, thereby attracting many enthusiastic advocates, including
myself. When discussing the actions that occur during a project, it is
convenient to use a "4Ps" terminology (the original 3Ps, plus one
I've added) that, in addition to being compact, is intrinsically clear because
the common meaning for each term is the intended meaning in ISM. The 4Ps
are preparing (reading,...), posing
(formulating a problem), probing (doing actions
to probe the problem and pursue a solution), and persuading.
INTERACTIONS BETWEEN ACTIVITIES AND STAGES.
The 4Ps can be viewed as 4 activities and as 4 stages, with interactions between
the activities and stages.
For example, persuading activity begins in
the posing stage. First, if problem constraints are chosen so they conform
to the evaluation criteria of the dominant scientific community, a solution
that satisfies these constraints is more likely to be accepted by other scientists.
Second, if action evaluation persuades a research group to pursue a solution
for a problem, the group may try to persuade a grant-funding agency that their
project is worthy of support.
Later, the persuading stage of a current
project can affect the posing stage of projects in the future, which are more
likely to be supported if the current persuasion can convince the community
that the current project (and its people and their problem-solving approach)
should be considered successful.
When are "plans for probing" made?
During the posing stage there is often some preliminary planning of actions
to solve the problem. Later, during the probing stage these plans are
modified and supplemented by improvised planning, done in response to the constantly
changing now-state. Finally, during the persuading stage, when it seems
that a solution has been achieved, there should be a rigorous self-critical
evaluation of one's own arguments for the proposed solution; this close
scrutiny often leads to a recognition of gaps in support, and to the planning
of additional probing activities for observation or interpretation.
The posing activity for a future project
can begin during any stage of a current project, whenever there is an idea for
a spinoff project whose goal is to solve a new problem. Similarly, at
any time there can be plans for immediate action to probe the current problem,
or delayed action to probe a different problem in the future.
INTERACTIONS BETWEEN AND WITHIN LEVELS.
A comprehensive history of science would see many groups working on a wide range
of interconnected projects over long periods of time. One aspect of this
grand story is the connections between projects, and between actions within
a project. These connections can be analyzed by examining different levels
of problems and problem-solving activity: mega-problem, problems, sub-problems,
and actions. Overlaps often occur within and between levels, with an extended
research group working on many problems and sub-problems simultaneously;
or several groups can work on the same problem or on different parts of a family
of related problems.
A group can increase the effectiveness of
its actions by coordinating its work on all of the sub-problems that contribute
to the solution of a larger problem. And if a group is working on several
problems simultaneously, an action may help to solve more than one problem.
Or projects can be related sequentially; work on a current project may inspire
ideas for a future project, and at the same time the current project is using
results from an earlier project while these results are being written up for
publication. A family of related projects, simultaneous or sequential,
can be produced by developing variations on a research theme.
Some of the most important interactions involve
knowledge. During a current project, scientists can search backward for
what they have learned (about observations and/or interpretations) from their
past work, or they can look forward to potential future uses for what is being
learned now, or sideways for possibilities of sharing knowledge among concurrent
research projects. Learning that occurs during research will help the
group that does the research, in their current and future projects. And
if a group's work is published or is shared informally among colleagues, their
experience can help other scientists learn.
8. Thought Styles
An Overview of Scientific Method, Section 8
This section describes what thought styles are, and how they affect the process and content of science.
A DEFINITION. As described by Grinnell (1992), a cell biologist
with an insider's view of science, a scientist's thought
style (or the collective thought style for
a group of scientists) is a system of concepts, developed from prior experience,
about nature and research science. It provides the "operating paradigm"
that guides decisions about what to study, and how to plan and do the research-actions
of observing and interpreting.
These concepts (about nature and science)
are related to the social and institutional structures within which they develop
and operate. But even though many ideas are shared in a scientific community,
some aspects of a thought style vary from one individual to another, and from
one group to another. There are interactions between groups, and each
individual belongs to many groups. { The following treatment will
not explicitly address this complexity, and will usually refer to "a thought
style" or "the thought style" as if only one style existed. }
EFFECTS ON OBSERVATION AND INTERPRETATION.
Thought styles affect the process and content of science.
The influence of a thought style may be difficult
to perceive because the ideas in it are often unconsciously assumed as "the
way things are done" rather than being explicitly stated. But these
ideas exist nevertheless, and they affect the process and content of science,
producing effects that span a wide range from the artistic taste that defines
a theory's "elegance" to the hard-nosed pragmatism of deciding whether
a project to develop a theory or explore a domain is worth the resources it
would require.
A thought style will influence (and when
viewed from another perspective, is comprised by) the problem-posing and problem-solving
strategies of individuals and groups. There may be a preference for projects
with comprehensive "know every step in advance" preliminary planning,
or casual "steer as you go" improvisational serendipity.
One procedural decision is to ask "Who
will do what during research?" Although it is possible for one scientist
to do all the activities in ISM, this is not necessary because within a research
group the efforts of individual scientists, each working on a different part
of the problem, can be cooperatively coordinated. Similarly, in a field
as a whole, each group can work on a different part of a mega-problem.
With a "division of labor," individuals or groups can specialize in
certain types of activities. One division is between experimentalists
who generate observations, and theorists who focus
on interpretation. But most scientists do some of both, with the balance
depending on the requirements of a particular research project and on the abilities
and preferences of colleagues.
There will be mutual influences between thought
styles and the procedural "rules of the game" developed by a community
of scientists to establish and maintain certain types of institutions and reward
systems, and procedures for deciding which people, topics, and viewpoints are
presented in conferences and are published in journals. A thought style
will affect attitudes toward competition and cooperation and how to combine
them effectively, and (at a community level) the ways in which activities of
different scientists and groups are coordinated. The logical and aesthetic
tastes of a community will affect the characteristics of written and oral presentations,
such as the blending of modes (verbal, visual, mathematical,...), the degree
of simplification, and the balance between abstractions and concrete illustrations
or analogies.
A thought style will tend to favor the production
of certain types of observation-and-interpretation knowledge rather than other
types. Effects on observation could include, for example, a preference
for either controlled experiments or field studies, and data collection that
is qualitative or quantitative. There will also be expectations for the
connections between experimenting and theorizing.
An intellectual environment will favor the
invention, pursuit and acceptance of certain types of theories. Some of
this influence arises from the design of experiments, which determines what
is studied and how, and thus the types of data collected. Another mechanism
for influence is the generation and selection of criteria for theory evaluation.
For example, thought styles can exert a strong influence on conceptual factors,
such as preferences for the types of components used in theories, the optimal
balance between simplicity and completeness, the value of unified wide-scope
theories, the relative importance of plausibility and utility, and the ways
in which a theory or project can be useful in promoting cognition and research.
Thought styles will influence, and will be influenced by, the goals of science,
such as whether the main goal of research projects should be to improve the
state of observations or interpretations, whether science should focus on understanding
nature or controlling nature, and what should be the relationships between science,
technology, and society.
The influence exerted by thought styles and cultural-personal factors is a hotly debated topic, as discussed on the EKS-Rated page.
CONCEPTUAL ECOLOGY. The metaphor of conceptual ecology (Toulmin, 1972) offers an interesting perspective on the effects of thought styles, based on analogy between biological and conceptual environments. In much the same way that the environmental characteristics of an ecological niche affect the natural selection occurring within its bounds, the intellectual characteristics of individuals — and of the dominant thought styles in the communities they establish and within which they operate — will favor the development and maintenance of certain types of ideas (about theories, experiments, goals, procedures,...) rather than others.
a PUZZLE and a FILTER. Bauer (1992)
compares science to solving a puzzle. In this metaphor (from Polanyi,
1962) scientists are assembling a jigsaw puzzle of
knowledge about nature, with the semi-finished puzzle in the open for all to
see. When
one scientist fits a piece into the puzzle, or modifies a piece already
in place,
others respond to this change by thinking about the next step that now becomes
possible. The overall result of these mutual adjustments is that the
independent activities of many scientists are coordinated so they blend
together and form
a structured cooperative whole.
Bauer supplements this portrait of science
with the metaphor of a filter, to describe the
process in which semi-reliable work done by scientists on the frontiers of research,
which Bauer describes in a way reminiscent of the "anything goes"
anti-method anarchy of Feyerabend (1975), is refined into the generally reliable
body of knowledge that appears in textbooks. In science, filtering occurs
in a perpetual process of self-correction, as individual inadequacies and errors
are filtered through the sieve of public accountability by collaborators and
colleagues, journal editors and referees, and by the community of scientists
who read journal articles, listen to conference presentations, and evaluate
what they read and hear. During this process it is probable, but not guaranteed,
that much of the effect of biased self-interest by one individual or group will
be offset by the actions of other groups. Due to this filtering, "textbook
knowledge" in the classroom is generally more reliable than "research
knowledge" at the frontiers, and the objectivity of science as a whole
is greater than the objectivity of its individual participants. { But
a byproduct of filtering, not directly acknowledged by Bauer, is that the collective
evaluations and dominant thought styles of a scientific community introduce
a "community bias" into the process and content of science. }
THE 4Ps AND THOUGHT STYLES. The puzzle
and filter metaphors provide useful ways to visualize posing and
persuading, respectively. While scientists watch what others are
doing with the puzzle of knowledge, they search for gaps to fill, for opportunities
to pose a problem where an investment of their own resources is likely to be
productive. And the process of filtering is useful for describing the
overall process of scientific persuasion, including its institutional procedures.
PREPARATION. There are
mutual influences between thought styles and three ways to learn. First,
the formal education of students who will become future scientists is affected
by the thought styles of current scientists and educators; in this way, current
science education helps to shape thought styles in the future. Second,
thought styles influence what scientists learn from their own past and current
research experience, to use in future research. Third, thought styles
influence the types of ideas that survive the "filtering" process
and are published in journals and textbooks.
POSING. The thought style
of a scientific community will affect every aspect of posing a problem: selecting
an area to study, forming perceptions about the current state of knowledge in
this area, and defining a desired goal-state for knowledge in the future.
Problem posing is important within science, and it plays a key role in the mutual
interactions between science and society by influencing both of the main ways
that science affects culture. First, posing affects the investment of
societal resources and the returns (such as medical-technological applications)
that may arise from these investments. Second, the questions asked by
science, and the constraints on how these questions are answered, will help
to shape cultural worldviews, concepts, and thinking patterns.
PROBING. As described
above, both types of probing activities — observation and interpretation —
are influenced by thought styles.
PERSUASION. For effective
persuasion, arguments should be framed in the structure of current knowledge
(so ideas can be more easily understood and appreciated by readers or listeners),
with an acceptable style of presentation, in a way that will be convincing when
judged by the standards of the evaluators, by carefully considering all factors
— empirical, conceptual, and cultural-personal — that may influence the evaluation
process at the levels of individuals and communities. Doing all of these
things skillfully requires a good working knowledge of the thought styles in
a scientific culture.
VARIATIONS. Thought styles vary from
one field of science to another, and so does their influence on the process
and content of science. For example, the methodology of chemistry emphasizes
controlled experiments, while geology and astronomy (or paleontology,...) depend
mainly on observations from field studies. And experiments in social science
and medical science, which typically use a relatively small number of subjects,
must be interpreted using a sophisticated analysis of sampling and statistics,
by contrast with the statistical simplicity of chemistry experiments that involve
a huge number of molecules.
Differences between fields could be caused
by a variety of contributing factors, including: 1) intrinsic differences
in the areas of nature being studied; 2) differences in the observational
techniques available for studying each area; 3) differences, due
to self selection, in the cognitive styles, personalities, values, and metaphysical-ideological
beliefs of scientists who choose to enter different fields; 4) historical
contingencies.
CHANGE. A model that is useful for analyzing change in science is proposed by Laudan (1984), whose "reticulated model of scientific rationality" is based on the mutual interactions between the goals, theories, and methods of scientists. When a change in one of these produces a dissonant relationship between between any of them, in order to reduce the dissonance there will be a motivation to make adjustments that will improve the overall logical harmony. {examples}
Variation and change are a part of science, and the study of methodological diversity and transformation can be fascinating and informative. But these characteristics of science should be viewed in proper perspective. It is important to balance a recognition of differences with an understanding of similarities, with an appreciation of the extent to which differences can be explained as "variations on a theme" — as variations on the basic methods shared by all scientists.
COMMUNITIES IN CONFLICT. One interesting
example of variation was a competition, beginning in 1961, to explain the phenomenon
of oxidative phosphorylation in mitochondria. In 1960 the widely accepted
explanation assumed the existence of a chemical intermediate. Even
though an intermediate had never been found, its eventual discovery was confidently
predicted, and this theory "was...considered an established fact of science.
(Wallace, et al, 1986; p 140)" But in 1961 Peter Mitchell proposed
an alternative theory based on a principle of chemiosmosis. Later,
a third competitor, energy transduction, entered the battle, and for
more than a decade these three theories — and their loyal defenders — were
involved in heated controversy.
This episode is a fascinating illustration
of contrasting thought styles, with radically different approaches to solving
the same problem. Advocates of each theory built their own communities,
each with its base of support from colleagues and institutions, and each with
its own assumptions and preferences regarding theories, experimental techniques,
and criteria for empirical and conceptual evaluation. All aspects of science
— including posing with its crucial question of which projects were most worthy
of support — were hotly debated due to the conflicting perspectives and the
corresponding differences in self-interest and in evaluations about the plausibility
and utility of each theory.
Eventually, chemiosmotic theory was declared
the winner, and in 1978 Mitchell was awarded the Nobel Prize in chemistry.
9. Productive Thinking
An Overview of Scientific Method, Section 9
Even though science occurs in the context of a community, it is done by individual scientists. Interactions with colleagues can stimulate productive ideas, but an idea always begins in the mind of an individual. The mental operations that occur within a scientist are summarized, in the ISM diagram, by "motivation and memory, creativity and critical thinking." Similar cognitive processes are involved, whether the focus of generation and evaluation is to produce an action (an experiment,...) or a theory.
MOTIVATION. Motivation inspires effort.
For a scientist, motivating factors include curiosity — such as asking (when
generating a theory) "What would nature be like if...? or (when generating
an experiment) "What would happen if we...?" — and a taste for intellectual
stimulation, along with practical concerns and psychological motives, such as
a desire to receive project funding or to be accepted into a prestigious professional
organization.
Often, necessity is the mother of invention.
For example, Newton invented a theory of calculus because he needed it to fill
a gap in the logical structure of his theory for celestial mechanics.
His immediate practical goal was finding a method to show that the gravitational
force produced by (or acting on) a spherically symmetric object is exactly the
same as if all the object's mass was concentrated at a point in the center of
the sphere. Calculus did show this, which enabled Newton's theory to make
easy calculations for the approximate forces acting on planetary objects.
Conversely, an absence of perceived need
can hinder invention. For example, there are clear benefits to having
more than one theory, because competition usually produces lively pursuit with
more testing that is designed to falsify a theory, and a more objective evaluation
with less danger of accepting a theory because "it's all we have."
But despite these benefits, usually a scientist who already has one theory will
not try to invent an alternative; based on a study of research in classical
genetics, Darden (1991, p. 268) found that "a single scientist usually
proposed one alternative and began testing predictions from it; other scientists
did likewise."
MEMORY. Although memory is not sufficient
for productive thinking, it is necessary to provide raw materials
(theories and exemplars, analogies and metaphors; experimental techniques and
systems/observations; problem-solving algorithms and heuristics,...) for processing
by creative, critical thinking.
For example, theory generation by either
selection or invention requires memory. With selection a theory is proposed
from memory. With invention a theory is proposed from imagination, but
this usually occurs by the revising or combining of existing ideas, in a mental
process that blends memory and imagination.
Productive thinking can be nourished by ideas
from a wide variety of sources. To build the solid foundation of knowledge
required for productive research, scientists engage in preparation by reading and listening, and learning from experience.
To stimulate and guide the process of thinking,
knowledge must be in the "working memory" of a scientist. There
are two ways to get knowledge into the mind: ideas can be retrieved from
internal storage in the scientist's long-term memory,
or they can be retrieved from external storage
in notes, articles or books, in computer memory (locally or on the internet),
or from the memory of colleagues.
CREATIVITY and CRITICAL THINKING. These two aspects of thinking are discussed in the same subsection because they complement each other, with a blending of both required for productive thinking. In defining creativity, Perkins (1984) emphasizes the criterion of productivity:
- Creative thinking is thinking patterned in a way that leads to creative results. ... The ultimate criterion for creativity is output. We call a person creative when that person consistently gets creative results, meaning, roughly speaking, original and otherwise appropriate results by the criteria of the domain in question. (pp. 18-19)
Of course, getting "appropriate results
by the criteria of the domain" requires critical evaluation. This
close connection between creativity and criticality is similar to the connections
between generation and evaluation. In fact, it can be useful to consider
generation and evaluation as the result of creative thinking and critical thinking,
respectively. This perspective is adopted in the "red plus blue makes
purple" color coding used in the ISM diagram: generation
plus evaluation yields productive
thinking in design. But this interpretation, although interesting,
is not logically rigorous, because a process of generation that is truly productive
(to get a high-quality idea, not just an idea) is usually guided by critical
evaluation, even in the initial stages, so equating generation with pure creativity
is not justified. Instead, it's better to consider the entire combination
of "motivation and memory, creativity and critical thinking" that
results in productive thinking with the generation of a theory (or experiment,
product, strategy, action,...) that is evaluated as being useful, and actually
is useful.
Considering the close connection between
creativity and criticality, perhaps a process of productive thinking that skillfully
combines creative and critical thinking could be called "creatical"
thinking? Well, maybe not. But calling it productive is
certainly appropriate.
The process of inventing
useful ideas requires both modes of thinking (creative and critical) but being
overly critical, especially in the early stages of invention, can stifle creativity. We
shouldn't hinder the motion of a car by driving with the brakes on, and we
shouldn't hinder the flow of creativity by thinking with restrictive criticism. But
a car needs brakes, and a creative person needs critical thinking. One
strategy for creativity is to "play games" with the modes by shifting
the balance in favor of creativity for awhile, by experimenting with different
balances between the modes during different stages in the overall process of
productive thinking.
For example, instruction designed to enhance
creative thinking often uses a technique of brainstorm
and edit. During an initial brainstorming
phase, critical restraints are minimized (this can be done in various
ways) to encourage a free creativity in generating lots of ideas; in a later editing
phase these ideas can be critically checked for plausibility and/or
utility. During the brainstorming phase, inventors can afford to think
freely (by consciously trying to see in a new way, to imagine new possibilities
without critical restrictions) because they have the security of knowing that
their wild ideas will not be acted on prematurely before these ideas have been
critically evaluated during the editing phase that follows. The principle
of this strategy is to allow the effective operation of both creativity and
criticality.
Productive thinking
often involves a tension between tradition and innovation. Sometimes
new ideas are needed, but often a skillful application of old ideas is the
key to success. Seeing from a new perspective, or perhaps just seeing
more clearly from a familiar perspective, can inspire the inventing of a new
idea or the remembering of an old idea. For example, when a new organic
compound is discovered (in nature) or synthesized (in the lab), instead of
inventing new experiments it may be more productive to use an existing methodology
consisting of a system of experiments that in the past have been useful for
exploring the properties of new compounds.
There may be a similar tension between
other contrasting virtues, such as persevering by tenacious hard work, or
flexibly deciding to stop wasting time on an approach that isn't working
and probably never will. A problem solver may need to dig deeper, so
perseverance is needed; but sometimes the key is to dig in a new location,
and flexibility (not perseverance) will pay off.
One of the most important actions in science (or in life) is to recognize an opportunity and take advantage of it, whether this involves observation or interpretation. In science the imaginative use of available observation detectors — either mechanical or human, for controlled experiments or planned field studies, for expected or unexpected results — can be highly effective in converting available information into recorded data. Following this, an insightful interpretation of observations can harvest more meaning from the raw data. Sherlock Holmes, with his alert awareness, careful observations, and clever interpretations, provides a fictional illustration of the benefits arising from an effective gathering and processing of all available information. Of course, being aware, careful, and clever are also valuable assets for a real scientist.
ENDNOTES
two examples of "reticulated" change in science:
Conceptual criteria are formulated and adopted
by people, and can be changed by people. In 1600, noncircular motion in
theories of astronomy was considered inappropriate, but in 1700 it was acceptable.
What caused this change? The theories of Kepler and Newton. First,
Kepler formulated a description of planetary motions with orbits that were elliptical,
not circular. Later, Newton provided a theoretical explanation for Kepler's
elliptical orbits by showing how they can be derived by combining his own laws
of motion and principle of universal gravitation. For a wide range of
reasons, scientists considered these theories — which postulated noncircular
celestial motions — to be successful, both empirically and conceptually, so
the previous prohibition of noncircular motions was abandoned. In this
case the standard portrait of science was reversed. Instead of using permanently
existing criteria to evaluate proposed theories, already-accepted theories were
used to evaluate and revise the evaluation criteria.
Laudan (1977, 1984) describes a similar situation,
with conflict between two beliefs, but this time the resolving of dissonance
resulted in a more significant change, a change in the fundamental epistemological
foundations of science. Some early interpretations of Newton's methods
claimed that he rigidly adhered to building theories by inductive generalization
from observations, and refused to indulge in hypothetical speculation.
Although these claims are disputed by most modern analyses, they were influential
in the early 1700s, and the apparently Newtonian methods were adopted by scientists
who tried to continue Newton's development of empiricist
theories (with core components derived directly from experience), and philosophers
developed empiricist theories of knowledge. But by the 1750s it was becoming
apparent that many of the most successful theories, in a variety of fields,
depended on the postulation of unobservable entities. There was a conflict
between these theories of science and the explicitly empiricist goals of science.
Rather than give up their non-empiricist theories, the scientists and philosophers
"sought to legitimate the aim of understanding the visible world by means
of postulating an invisible world whose behavior was causally responsible for
what we do observe. ... To make good on their proposed aims, they had
to develop a new methodology of science,... the hypothetico-deductive method.
Such a method allowed for the legitimacy of hypotheses referring to theoretical
entities, just so long as a broad range of correct observational claims could
be derived from such hypotheses. (Laudan, 1984; p. 57)"
what it is:
Integrated Scientific Method (ISM) is a model of
scientific action.
It is a synthesis of ideas — mainly from scientists and philosophers,
but also from sociologists, psychologists, historians, and myself — that
describes the activities of scientists: what they think about and what they
do.
It shows how the mutually supportive skills of creativity and critical thinking
are intimately integrated in the problem-solving methods used by scientists.
and what it is not:
Because I agree with the consensus that no single "method" is used
by
all scientists at all times, I am not trying to define the scientific
method.
Therefore, it is most accurate (and most useful)
to view ISM,
not as a rigorous flowchart for describing a predictable sequence,
but as a roadmap that shows possibilities for creative wandering.
ISM is mainly intended to help people understand
science and
to be useful for education (for teachers and students,
and designers of "thinking skills" instruction),
not for a deep study of science by scholars.
smaller Overview of Scientific Method page
(with links to the detailed descriptions above),
followed by a visual representation in the ISM-diagram:
1. Hypothetico-Deductive
Logic, and Empirical Factors in Theory Evaluation In ISM an experimental system (for a controlled experiment or field study) is defined as everything involved in an experiment, including what is being studied, what is done to it, and the observers (which can be human or mechanical). When a physical experiment is done with the experimental system, observation detectors are used to obtain observations. A theory is
a humanly constructed representation intended to describe or explain
the observed phenomena in a specified domain of
nature. By using a general domain-theory (which
is claimed to be valid for all experimental systems in a domain,
and involves a theory plus a
foundation of supplementary theories)
combined with a specific system-theory (about
the characteristics of one experimental system), scientists construct
an explanatory model that is
a simplified representation of the system's composition (what
it is) and operation (what it does). After
defining an explanatory model (for composition-and-operation, made
by applying a general domain-theory to a specific experimental system
that has been characterized by a system-theory), a thought
experiment can be done by asking, "IF this model
is true, THEN what will occur?", thereby using deductive
logic to make predictions. Most of this page was written in 1997. Later,
in 2006, I said in the "Designing of Scientific Theories" section
of An Introduction
to Scientific Method, Later, I'll take the time to think about this more rigorously and will incorporate these concepts into the box above, to describe the relationships between different types of theories: domain, system, mini, and sub. The dual-parallel shape of the hypothetico-deductive "box" (whose 4 corners are defined by the model and system, predictions and observations) symbolizes two parallel relationships. The left-side process (done by mentally running a theory-based model) parallels the right-side process (done by physically running a real-world experimental system). There is also a parallel between the top and bottom of the box. At the top, a hypothesis is a claim that the model and system are similar in some respects and to some degree of accuracy. At the bottom is a logical comparison of predictions (by the model) and observations (of the system); this comparison is used to evaluate the hypothesis, based on the logic that the degree of agreement between predictions and observations may be related to the degree of similarity between model and system. But a theory can be false even if its predictions agree with observations, so it is necessary to supplement this "agreement logic" with another criterion, the degree of predictive contrast, by asking "How much contrast exists between the predictions of this theory and the predictions of plausible alternative theories?" in an effort to consider the possibility that two or more theories could make the same correct predictions for this system. Estimates for degrees of agreement and predictive contrast are combined to form an empirical evaluation of current hypothesis. This evaluation and the analogous empirical evaluations of previous hypotheses (that are based on the same theory as the current hypothesis) are empirical factors that influence theory evaluation. { the detailed version of Section 1 is available earlier in this page } 2. Conceptual
Factors in Theory Evaluation { the detailed version of Section 2 is available earlier in this page } 3. Cultural-Personal
Factors in Theory Evaluation { the detailed version of Section 3 is available earlier in this page } 4. Theory
Evaluation { the detailed version of Section 4 is available earlier in this page } 5. Theory Generation Generating a theory can involve selecting an old theory or, if necessary, inventing a new theory. The process of inventing a new theory usually occurs by revising an existing "old theory." Some strategies for invention are: split an old theory into components that can be modified or recombined in new ways; borrow components (or logical structure) from other theories; generalize an old theory, as-is or modified, into a new domain; or apply the logic of internal consistency to build on the foundation of a few assumed axiom-components. Often, a creative analysis of data (to search for patterns) is a key step in constructing a theory. Theory generation is guided by evaluation factors that are cultural-personal, conceptual, and empirical. There is a close relationship between the generation and evaluation of a theory. { Similarly, the generation and evaluation of an action (such as an experiment) are closely related. } Empirical guidance is used
in the creative-and-critical process of retroduction —
a thinking strategy in which the goal is to generate (to propose by selection
or invention) a theory whose predictions will match known
observations. If there is data from several experiments,
retroduction can aim for a theory whose predictions are consistent with all
known data. During retroduction a scientist, curious about puzzling
observations and motivated to find an explanation, can adjust either of the
two sources used to construct a model: a general domain-theory (that
applies to all systems in a domain) and a specific system-theory (about
the characteristics of one system). Usually, a scientific "inference to the best explanation" involves a creative
use of logic that is both inductive and deductive. { the detailed version of Section 5 is available earlier in this page } 6. Experimental
Design (Generation-and-Evaluation) Thought-experiments,
done to quickly explore a variety of possibilities, can help scientists evaluate
potential experimental systems and decide which ones are worthy of further
pursuit with physical experiments that typically require larger investments
of time and money. { the detailed version of Section 6 is available earlier in this page } 7. Problem-Solving
Projects { the detailed version of Section 7 is available earlier in this page } 8. Thought Styles { the detailed version of Section 8 is available earlier in this page } 9. Mental Operations { the detailed version of Section 9 is available earlier in this page } |