 Science
in Christian Perspective
Science
in Christian Perspective Science
in Christian Perspective
Science
in Christian Perspective
Radiometric Dating
A Christian Perspective
Dr. Roger C. Wiens
941 Estates Drive, Los Alamos, NM 87544
RCWiens@MSN.Com
Dr. Wiens has a PhD in Physics, with a minor in Geology. His PhD thesis was on isotope ratios in meteorites, including surface exposure dating. He was employed at Caltech's Division of Geological & Planetary Sciences at the time of writing the first edition. He is presently employed in the Space & Atmospheric Sciences Group at the Los Alamos National Laboratory.
First edition 1994; revised version 2002.
Radiometric dating--the process of determining the age of rocks from the decay of their radioactive elements--has been in widespread use for over half a century. There are over forty such techniques, each using a different radioactive element or a different way of measuring them. It has become increasingly clear that these radiometric dating techniques agree with each other and as a whole, present a coherent picture in which the Earth was created a very long time ago. Further evidence comes from the complete agreement between radiometric dates and other dating methods such as counting tree rings or glacier ice core layers. Many Christians have been led to distrust radiometric dating and are completely unaware of the great number of laboratory measurements that have shown these methods to be consistent. Many are also unaware that Bible-believing Christians are among those actively involved in radiometric dating.
This paper describes in relatively simple terms how a number of the dating techniques work, how accurately the half-lives of the radioactive elements and the rock dates themselves are known, and how dates are checked with one another. In the process the paper refutes a number of misconceptions prevalent among Christians today. This paper is available on the web via the American Scientific Affiliation and related sites to promote greater understanding and wisdom on this issue, particularly within the Christian community.
ii
TABLE OF CONTENTS
Introduction
Overview
The Radiometric Clocks
Examples of Dating Methods for Igneous Rocks
Potassium-Argon
Argon-Argon
Rubidium-Strontium
Samarium-Neodymium, Lutetium-Hafnium, and Rhenium-Osmium
Uranium-Lead
The Age of the Earth
Extinct Radionuclides: The Hourglasses that Ran Out
Cosmogenic Radionuclides: Carbon-14, Beryllium-10, Chlorine-36
Radiometric Dating of Geologically Young Samples
Non-Radiogenic Dating Methods for the Past 100,000 Years
Ice Cores
Varves
Other Annual-Layering Methods
Thermoluminescence
Electron Spin Resonance
Cosmic Ray Exposure Dating
Can We Really Believe the Dating Systems?
Doubters Still Try
Apparent Age?
Rightly Handling the Word of Truth
Appendix: Common Misconceptions Regarding Radiometric Dating
Techniques
Resources on the Web
Further Reading: Books
Acknowledgements
More About the Author
Glossary
Introduction
Arguments over the age of the Earth have sometimes been divisive for people who regard the Bible as God's word. Even though the Earth's age is never mentioned in the Bible, it is an issue because those who take a strictly literal view of the early chapters of Genesis can calculate an approximate date for the creation by adding up the life-spans of the people mentioned in the genealogies. Assuming a strictly literal interpretation of the week of creation, even if some of the generations were left out of the genealogies, the Earth would be less than ten thousand years old. Radiometric dating techniques indicate that the Earth is thousands of times older than that--approximately four and a half billion years old. Many Christians accept this and interpret the Genesis account in less scientifically literal ways. However, some Christians suggest that the geologic dating techniques are unreliable, that they are wrongly interpreted, or that they are confusing at best. Unfortunately, much of the literature available to Christians has been either inaccurate or difficult to understand, so that confusion over dating techniques continues.
The next few pages cover a broad overview of radiometric
dating techniques, show a few examples, and discuss the degree to which the
various dating systems agree with each other. The goal is to promote greater
understanding on this issue, particularly for the Christian community. Many
people have been led to be skeptical of dating without knowing much about it.
For example, most people don't realize that carbon dating is only rarely used on
rocks. God has called us to be "wise as serpents" (Matt. 10:16) even
in this scientific age. In spite of this, differences still occur within the
church. A disagreement over the age of the Earth is relatively minor in the
whole scope of Christianity; it is more important to agree on the Rock of Ages
than on the age of rocks. But because God has also called us to wisdom, this
issue is worthy of study.
Overview
Rocks are made up of many individual crystals, and each crystal is usually made up of at least several different chemical elements such as iron, magnesium, silicon, etc. Most of the elements in nature are stable and do not change. However, some elements are not completely stable in their natural state. Some of the atoms eventually change from one element to another by a process called radioactive decay. If there are a lot of atoms of the original element, called the parent element, the atoms decay to another element, called the daughter element, at a predictable rate. The passage of time can be charted by the reduction in the number of parent atoms, and the increase in the number of daughter atoms.
Radiometric dating can be compared to an hourglass. When the glass is turned over, sand runs from the top to the bottom. Radioactive atoms are like individual grains of sand--radioactive decays are like the falling of grains from the top to the bottom of the glass. You cannot predict exactly when any one particular grain will get to the bottom, but you can predict from one time to the next how long the whole pile of sand takes to fall. Once all of the sand has fallen out of the top, the hourglass will no longer keep time unless it is turned over again. Similarly, when all the atoms of the radioactive element are gone, the rock will no longer keep time (unless it receives a new batch of radioactive atoms).
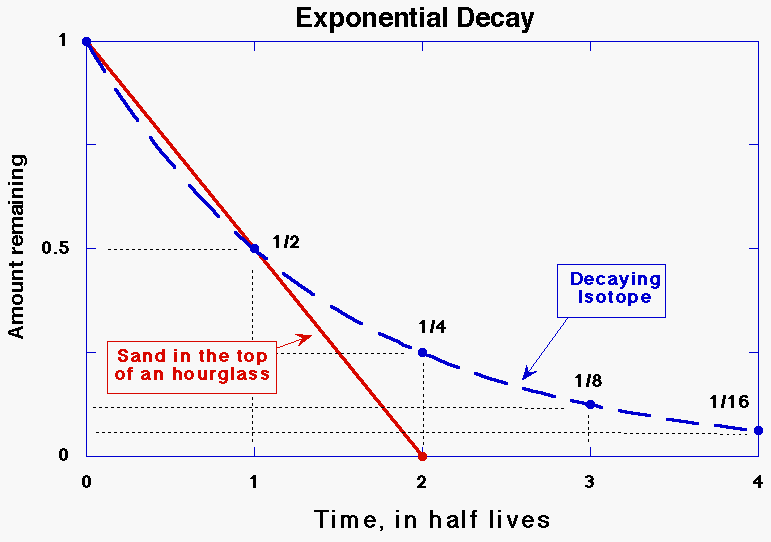
|
Unlike the hourglass, where the amount of sand falling is constant right up until the end, the number of decays from a fixed number of radioactive atoms decreases as there are fewer atoms left to decay (see Figure 1). If it takes a certain length of time for half of the atoms to decay, it will take the same amount of time for half of the remaining atoms, or a fourth of the original total, to decay. In the next interval, with only a fourth remaining, only one eighth of the original total will decay. By the time ten of these intervals, or half-lives, has passed, less than one thousandth of the original number of radioactive atoms is left. The equation for the fraction of parent atoms left is very simple. The type of equation is exponential, and is related to equations describing other well-known phenomena such as population growth. No deviations have yet been found from this equation for radioactive decay.
Also unlike the hourglass, there is no way to change the rate at which radioactive atoms decay in rocks
. If you shake the hourglass, twirl it, or put it in a rapidly accelerating vehicle, the time it takes the sand to fall will change. But the radioactive atoms used in dating techniques have been subjected to heat, cold, pressure, vacuum, acceleration, and strong chemical reactions to the extent that would be experienced by rocks or magma in the mantle, crust, or surface of the Earth or other planets without any significant change in their decay rate.An hourglass will tell time correctly only if it is completely sealed
. If it has a hole allowing the sand grains to escape out the side instead of going through the neck, it will give the wrong time interval. Similarly, a rock that is to be dated must be sealed against loss or addition of either the radioactive daughter or parent. If it has lost some of the daughter element, it will give an inaccurately young age. As will be discussed later, most dating techniques have very good ways of telling if such a loss has occurred, in which case the date is thrown out (and so is the rock!).An hourglass measures how much time has passed since it was turned over. (Actually it tells when a specific amount of time, e.g., 2 minutes, an hour, etc., has passed, so the analogy is not quite perfect.) Radiometric dating of rocks also tells how much time has passed since some event occurred. For igneous rocks the event is usually its cooling and hardening from magma or lava. For some other materials, the event is the end of a metamorphic heating event (in which the rock gets baked underground at generally over a thousand degrees Fahrenheit), the uncovering of a surface by the scraping action of a glacier, the chipping of a meteorite off of an asteroid, or the length of time a plant or animal has been dead.
The Radiometric Clocks
There are now well over forty different radiometric dating techniques, each based on a different radioactive isotope.
The term isotope subdivides elements into groups of atoms that have the same atomic weight. For example carbon has isotopes of weight 12, 13, and 14 times the mass of a nucleon, referred to as carbon-12, carbon-13, or carbon-14 (abbreviated as 12C, 13C, 14C). It is only the carbon-14 isotope that is radioactive. This will be discussed further in a later section.
A partial list of the parent and daughter isotopes and the decay half-lives is given in Table I. Notice the large range in the half-lives. Isotopes with long half-lives decay very slowly, and so are useful for dating
|
Table 1. Some Naturally Occurring Radioactive Isotopes and their half-lives | ||||||||||||||||||||||||||||||||||||||||||
| ||||||||||||||||||||||||||||||||||||||||||
|
|
correspondingly ancient events. Isotopes with shorter half-lives cannot date very ancient events because all of the atoms of the parent isotope would have already decayed away, like an hourglass left sitting with all the sand at the bottom. Isotopes with relatively short half-lives are useful for dating correspondingly shorter intervals, and can usually do so with greater accuracy, just as you would use a stopwatch rather than a grandfather clock to time a 100 meter dash. On the other hand, you would use a calendar, not a clock, to record time intervals of several weeks or more.
The half-lives have all been measured directly either by using a radiation detector to count the number of atoms decaying in a given amount of time from a known amount of the parent material, or by measuring the ratio of daughter to parent atoms in a sample that originally consisted completely of parent atoms. Work on radiometric dating first started shortly after the turn of the 20th century, but progress was relatively slow before the late
forties. However, by now we have had over fifty years to measure and re-measure the half-lives for many of the dating techniques. Very precise counting of the decay events or the daughter atoms can be done, so while the number of, say, rhenium-187 atoms decaying in 50 years is a very small fraction of the total, the resulting osmium-187 atoms can be very precisely counted. For example, recall that only one gram of material contains over 1021 (1 with 21 zeros behind) atoms. Even if only one trillionth of the atoms decay in one year, this is still millions of decays, each of which can be counted by a radiation detector!
The uncertainties on the half-lives given in the table are all very small. All of the half-lives are known to better than about two percent except for rhenium (5%), lutetium (3%), and beryllium (3%). There is no evidence of any of the half-lives changing over time. In fact, as discussed below, they have been observed to not change at all over hundreds of thousands of years.
Examples of Dating Methods for Igneous Rocks
Now let's look at how the actual dating methods work. Igneous rocks are good candidates for dating. Recall that for igneous rocks the event being dated is when the rock was formed from magma or lava. When the molten material cools and hardens, the atoms are no longer free to move about. Daughter atoms that result from radioactive decays occurring after the rock cools are frozen in the place where they were made within the rock. These atoms are like the sand grains accumulating in the bottom of the hourglass. Determining the age of a rock is a two-step process. First one needs to measure the number of daughter atoms and the number of remaining parent atoms and calculate the ratio between them. Then the half-life is used to calculate the time it took to produce that ratio of parent atoms to daughter atoms.
However, there is one complication. One cannot always assume that there were no daughter atoms to begin with. It turns out that there are some cases where one can make that assumption quite reliably. But in most cases the initial amount of the daughter product must be accurately determined. Most of the time one can use the different amounts of parent and daughter present in different minerals within the rock to tell how much daughter was originally present. Each dating mechanism deals with this problem in its own way. Some types of dating work better in some rocks; others are better in other rocks, depending on the rock composition and its age. Let's examine some of the different dating mechanisms now.
Potassium-Argon. Potassium is an abundant element in the Earth's crust. One isotope, potassium-40, is radioactive and decays to two different daughter products, calcium-40 and argon-40, by two different decay methods. This is not a problem because the production ratio of these two daughter products is precisely known, and is always constant: 11.2% becomes argon-40 and 88.8% becomes calcium-40. It is possible to date some rocks by the potassium-calcium method, but this is not often done because it is hard to determine how much calcium was initially present. Argon, on the other hand, is a gas. Whenever rock is melted to become magma or lava, the argon tends to escape. Once the molten material hardens, it begins to trap the new argon produced since the hardening took place. In this way the potassium-argon clock is clearly reset when an igneous rock is formed.
In its simplest form, the geologist simply needs to measure the relative amounts of potassium-40 and argon-40 to date the rock. The age is given by a relatively simple equation:
t = h x ln[1 + (argon-40)/(0.112 x (potassium-40))]/ln(2)
where t is the time in years, h is the half-life, also in years, and ln is the natural logarithm.
However, in reality there is often a small amount of argon remaining in a rock when it hardens. This is usually trapped in the form of very tiny air bubbles in the rock. One percent of the air we breathe is argon. Any extra argon from air bubbles may need to be taken into account if it is significant relative to the amount of radiogenic argon (that is, argon produced by radioactive decays). This would most likely be the case in either young rocks that have not had time to produce much radiogenic argon, or in rocks that are low in the parent potassium. One must have a way to determine how much air-argon is in the rock. This is rather easily done because air-argon has a couple of other isotopes, the most abundant of which is argon-36. The ratio of argon-40 to argon-36 in air is well known, at 295. Thus, if one measures argon-36 as well as argon-40, one can calculate and subtract off the air-argon-40 to get an accurate age.
One of the best ways of showing that an age-date is correct is to confirm it with one or more different dating
| Some young-Earth proponents recently reported that rocks were dated by the potassium-argon method to be a several million years old when they are really only a few years old. But the potassium-argon method, with its long half-life, was never intended to date rocks only 25 years old. These people have only succeeded in correctly showing that one can fool a single radiometric dating method when one uses it improperly. The false radiometric ages of several million years are due to parentless argon, as described here, and first reported in the literature some fifty years ago. Note that it would be extremely unlikely for another dating method to agree on these bogus ages. Getting agreement between more than one dating method is a recommended practice. |
method(s). Although potassium-argon is one of the simplest dating methods, there are still some cases where it does not agree with other methods. When this does happen, it is usually because the gas within bubbles in the rock is from deep underground rather than from the air. This gas can have a higher concentration of argon-40 escaping from the melting of older rocks. This is called parentless argon-40 because its parent potassium is not in the rock being dated, and is also not from the air. In these slightly unusual cases, the date given by the normal potassium-argon method is too old. However, scientists in the mid-1960s came up with a way around this problem, the argon-argon method, discussed in the next section.
Argon-Argon. Even though it has been around for nearly half a century, the argon-argon method is seldom discussed by groups critical of dating methods. This method uses exactly the same parent and daughter isotopes as the potassium-argon method. In effect, it is a different way of telling time from the same clock. Instead of simply comparing the total potassium with the non-air argon in the rock, this method has a way of telling exactly what and how much argon is directly related to the potassium in the rock.
In the argon-argon method the rock is placed near the center of a nuclear reactor for a period of hours. A nuclear reactor emits a very large number of neutrons, which are capable of changing a small amount of the potassium-39 into argon-39. Argon-39 is not found in nature because it has only a 269-year half-life. (This half-life doesn't affect the argon-argon dating method as long as the measurements are made within about five years of the neutron dose). The rock is then heated in a furnace to release both the argon-40 and the argon-39 (representing the potassium) for analysis. The heating is done at incrementally higher temperatures and at each step the ratio of argon-40 to argon-39 is measured. If the argon-40 is from decay of potassium within the rock, it will come out at the same temperatures as the potassium-derived argon-39 and in a constant proportion. On the other hand, if there is some excess argon-40 in the rock it will cause a different ratio of argon-40 to argon-39 for some or many of the heating steps, so the different heating steps will not agree with each other.
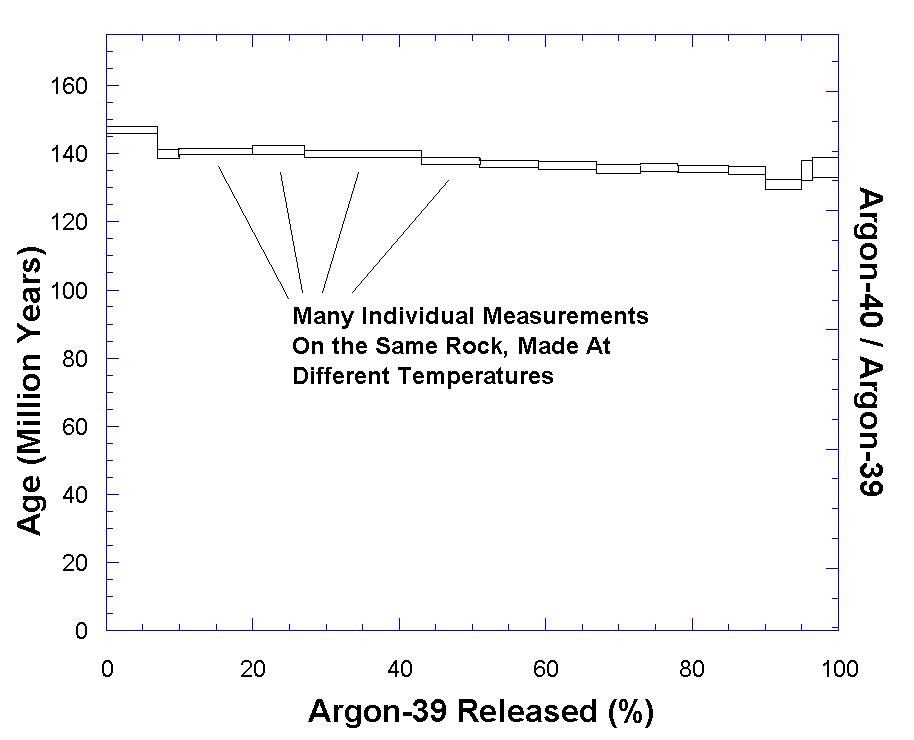 Figure 2. A typical argon-argon dating plot. Each small rectangle represents the apparent age given at one particular heating-step temperature. The top and bottom parts of the rectangles represent upper and lower limits for that particular determination. The age is based on the measured argon-40 / argon-39 ratio and the number of neutrons encountered in the reactor. The horizontal axis gives the amount of the total argon-39 released from the sample. A good argon-argon age determination will have a lot of heating steps which all agree with each other. The "plateau age" is the age given by the average of most of the steps, in this case nearly 140 million years. After S. Turner et al. (1994) Earth and Planetary Science Letters, 121, pp. 333-348. |
Figure 2 is an example of a good argon-argon date. The fact that this plot is flat shows that essentially all of the argon-40 is from decay of potassium within the rock. The potassium-40 content of the sample is found by multiplying the argon-39 by a factor based on the neutron exposure in the reactor. When this is done, the plateau in the figure represents an age date based on the decay of potassium-40 to argon-40.
There are occasions when the argon-argon dating method does not give an age even if there is sufficient potassium in the sample and the rock was old enough to date. This most often occurs if the rock experienced a high temperature (usually a thousand degrees Fahrenheit or more) at some point since its formation. If that occurs, some of the argon gas moves around, and the analysis does not give a smooth plateau across the extraction temperature steps. An example of an argon-argon analysis that did not yield an age date is shown in Figure 3. Notice that there is no good plateau in this plot. In some instances there will actually be two plateaus, one representing the formation age, and another representing the time at which the heating episode occurred. But in most cases where the system has been disturbed, there simply is no date given. The important point to note is that, rather than giving wrong age dates, this method simply does not give a date if the system has been disturbed. This is also true of a number of other igneous rock dating methods, as we will describe below.
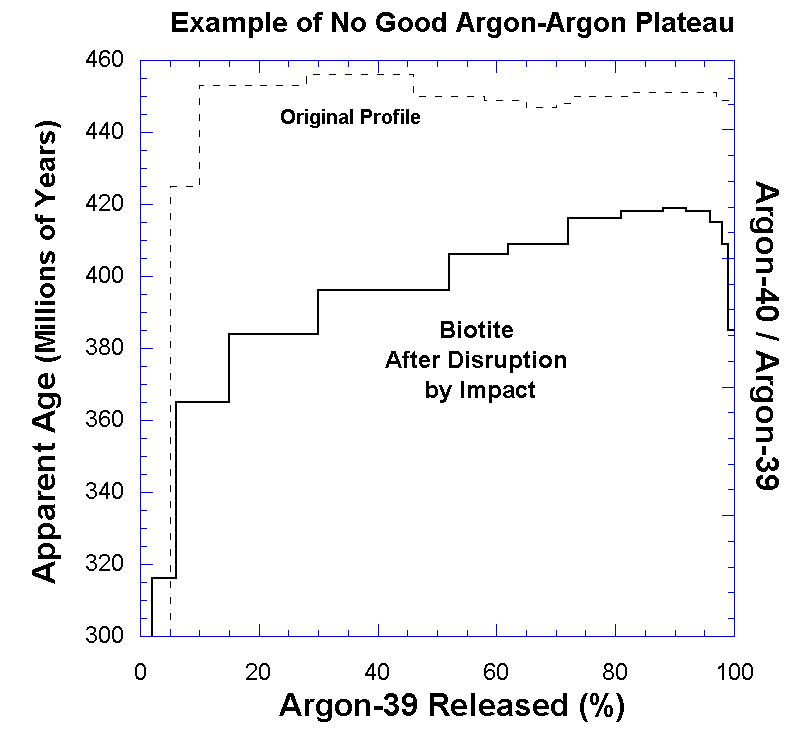
Figure 3.
Rubidium-Strontium. In nearly all of the dating methods, except potassium-argon and the associated argon-argon method, there is always some amount of the daughter product already in the rock when it cools. Using these methods is a little like trying to tell time from an hourglass that was turned over before all of the sand had fallen to the bottom. One can think of ways to correct for this in an hourglass: One could make a mark on the outside of the glass where the sand level started from and then repeat the interval with a stopwatch in the other hand to calibrate it. Or if one is clever she or he could examine the hourglass' shape and determine what fraction of all the sand was at the top to start with. By knowing how long it takes all of the sand to fall, one could determine how long the time interval was. Similarly, there are good ways to tell quite precisely how much of the daughter product was already in the rock when it cooled and hardened.
In the rubidium-strontium method, rubidium-87 decays with a half-life of 48.8 billion years to strontium-87. Strontium has several other isotopes that are stable and do not decay. The ratio of strontium-87 to one of the other stable isotopes, say strontium-86, increases over time as more rubidium-87 turns to strontium-87. But when the rock first cools, all parts of the rock have the same strontium-87/strontium-86 ratio because the isotopes were mixed in the magma. At the same time, some of the minerals in the rock have a higher rubidium/strontium ratio than others. Rubidium has a larger atomic diameter than strontium, so rubidium does not fit into the crystal structure of some minerals as well as others.Figure 4 is an important type of plot used in rubidium-strontium dating. It shows the strontium-87/strontium-86 ratio on the vertical axis and the
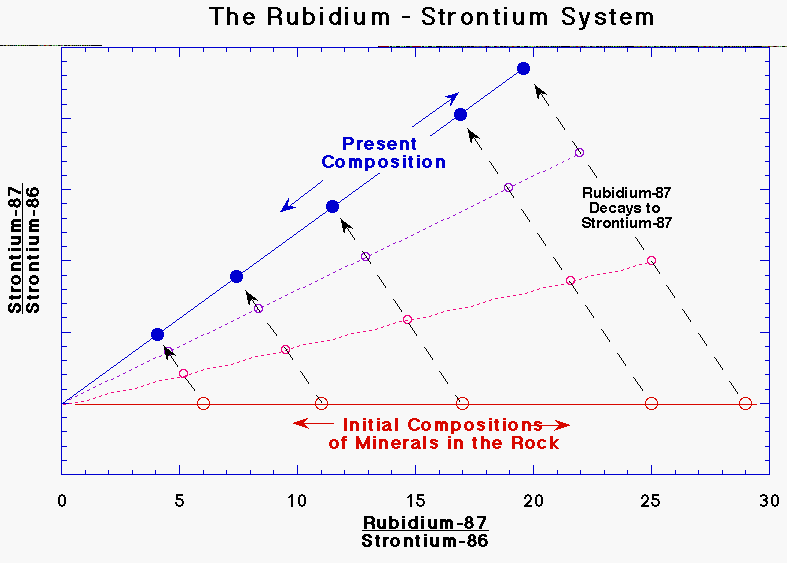 Figure 4. A rubidium-strontium three-isotope plot. When a rock cools, all its minerals have the same ratio of strontium-87 to strontium-86, though they have varying amounts of rubidium. As the rock ages, the rubidium decreases by changing to strontium-87, as shown by the dotted arrows. Minerals with more rubidium gain more strontium-87, while those with less rubidium do not change as much. Notice that at any given time, the minerals all line up--a check to ensure that the system has not been disturbed. |
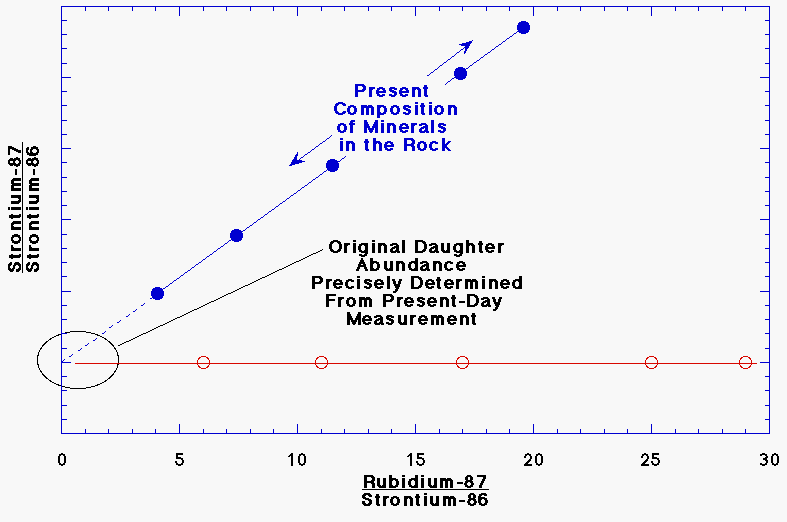
Figure 5. The original amount of the daughter strontium-87 can be precisely determined from the present-day composition by extending the line through the data points back to rubidium-87 = 0. This works because if there were no rubidium-87 in the sample, the strontium composition would not change. The slope of the line is used to determine the age of the sample.
rubidium-87/strontium-86 ratio on the horizontal axis, that is, it plots a ratio of the daughter isotope against a ratio of the parent isotope. At first, all the minerals lie along a horizontal line of constant strontium-87/strontium-86 ratio but with varying rubidium/strontium. As the rock starts to age, rubidium gets converted to strontium. The amount of strontium added to each mineral is proportional to the amount of rubidium present. This change is shown by the dashed arrows, the lengths of which are proportional to the rubidium/strontium ratio. The dashed arrows are slanted because the rubidium/strontium ratio is decreasing in proportion to the increase in strontium-87/strontium-86. The solid line drawn through the samples will thus progressively rotate from the horizontal to steeper and steeper slopes.
All lines drawn through the data points at any later time will intersect the horizontal line (constant strontium-87/strontium-86 ratio) at the same point in the lower left-hand corner. This point, where rubidium-87/strontium-86 = 0 tells the original strontium-87/strontium-86 ratio. From that we can determine the original daughter strontium-87 in each mineral, which is just what we need to know to determine the correct age.
It also turns out that the slope of the line is proportional to the age of the rock. The older the rock, the steeper the line will be. If the slope of the line is m and the half-life is h, the age t (in years) is given by the equation
t = h x ln(m+1)/ln(2)
For a system with a very long half-life like rubidium-strontium, the actual numerical value of the slope will always be quite small. To give an example for the above equation, if the slope of a line in a plot similar to Fig. 4 is m = 0.05110 (strontium isotope ratios are usually measured very accurately--to about one part in ten thousand),
we can substitute in the half-life (48.8 billion years) and solve as follows:
t = (48.8) x ln(1.05110)/ln(2)
so t = 3.51 billion years.
Several things can on rare occasions cause problems for the rubidium-strontium dating method. One possible source of problems is if a rock contains some minerals that are older than the main part of the rock. This can happen when magma inside the Earth picks up unmelted minerals from the surrounding rock as the magma moves through a magma chamber. Usually a good geologist can distinguish these "xenoliths" from the younger minerals around them. If he or she does happen to use them for dating the rock, the points represented by these minerals will lie off the line made by the rest of the points. Another difficulty can arise if a rock has undergone metamorphism, that is, if the rock got very hot, but not hot enough to completely re-melt the rock. In these cases, the dates look confused, and do not lie along a line. Some of the minerals may have completely melted, while others did not melt at all, so some minerals try to give the igneous age while other minerals try to give the metamorphic age. In these cases there will not be a straight line, and no date is determined.
In a few very rare instances the rubidium-strontium method has given straight lines that give wrong ages. This can happen when the rock being dated was formed from magma that was not well mixed, and which had two distinct batches of rubidium and strontium. One magma batch had rubidium and strontium compositions near the upper end of a line (such as in Fig. 4), and one batch had compositions near the lower end of the line. In this case, the
minerals all got a mixture of these two batches, and their resulting composition ended up near a line between the two batches. This is called a two-component mixing line. It is a very rare occurrence in these dating mechanisms, but at least thirty cases have been documented among the tens of thousands of rubidium-strontium dates made. If
a two-component mixture is suspected, a second dating method must be used to confirm or disprove the rubidium-strontium date. The agreement of several dating methods is the best fail-safe way of dating rocks.
The Samarium-Neodymium, Lutetium-Hafnium, and Rhenium-Osmium Methods. All of these methods work very similarly to the rubidium-strontium method. They all use three-isotope diagrams similar to Figure 4 to determine the age. The samarium-neodymium method is the most-often used of these three. It uses the decay of samarium-147 to neodymium-143, which has a half-life of 105 billion years. The ratio of the daughter isotope, neodymium-143, to another neodymium isotope, neodymium-144, is plotted against the ratio of the parent, samarium-147, to neodymium-144. If different minerals from the same rock plot along a line, the slope is determined, and the age is given by the same equation as above. The samarium-neodymium method may be preferred for rocks that have very little potassium and rubidium, for which the potassium-argon, argon-argon, and rubidium-strontium methods might be difficult. The samarium-neodymium method has also been shown to be more resistant to being disturbed or re-set by metamorphic heating events, so for some metamorphosed rocks the samarium-neodymium method is preferred. For a rock of the same age, the slope on the neodymium-samarium plots will be less than on a rubidium-strontium plot because the half-life is longer. However, these isotope ratios are usually measured to extreme accuracy--several parts in ten thousand--so accurate dates can be obtained even for ages less than one fiftieth of a half-life, and with correspondingly small slopes.
The lutetium-hafnium method uses the 38 billion year half-life of lutetium-176 decaying to hafnium-176. This dating system is similar in many ways to samarium-neodymium, as the elements tend to be concentrated in the same types of minerals. Since samarium-neodymium dating is somewhat easier, the lutetium-hafnium method is used less often.
The rhenium-osmium method takes advantage of the fact that the osmium concentration in most rocks and minerals is very low, so a small amount of the parent rhenium-187 can produce a significant change in the osmium isotope ratio. The half-life for this radioactive decay is 42 billion years. The non-radiogenic stable isotopes, osmium-186 or -188, are used as the denominator in the ratios on the three-isotope plots. This method has been useful for dating iron meteorites, and is now enjoying greater use for dating Earth rocks due to development of easier rhenium and osmium isotope measurement techniques.
Uranium-Lead and related techniques. The uranium-lead method is the longest-used dating method. It was first used in 1907, about a century ago. The uranium-lead system is more complicated than other parent-daughter systems; it is actually several dating methods put together. Natural uranium consists primarily of two isotopes, U-235 and U-238, and these isotopes decay with different half-lives to produce lead-207 and lead-206, respectively. In addition, lead-208 is produced by thorium-232. Only one isotope of lead, lead-204, is not radiogenic. The uranium-lead system has an interesting complication: none of the lead isotopes is produced directly from the uranium and thorium. Each decays through a series of relatively short-lived radioactive elements that each decay to a lighter element, finally ending up at lead. Since these half-lives are so short compared to U-238, U-235, and thorium-232, they generally do not affect the overall dating scheme. The result is that one can obtain three independent estimates of the age of a rock by measuring the lead isotopes and their parent isotopes. Long-term dating based on the U-238, U-235, and thorium-232 will be discussed briefly here; dating based on some of the shorter-lived intermediate isotopes is discussed later.
The uranium-lead system in its simpler forms, using U-238, U-235, and thorium-232, has proved to be less reliable than many of the other dating systems. This is because both uranium and lead are less easily retained in many of the minerals in which they are found. Yet the fact that there are three dating systems all in one allows scientists to easily determine whether the system has been disturbed or not. Using slightly more complicated mathematics, different combinations of the lead isotopes and parent isotopes can be plotted in such a way as to
minimize the effects of lead loss. One of these techniques is called the lead-lead technique because it determines the ages from the lead isotopes alone. Some of these techniques allow scientists to chart at what points in time metamorphic heating events have occurred, which is also of significant interest to geologists.
|
|||||||||||||||||||||||||||||||
The Age of the Earth
We now turn our attention to what the dating systems tell us about the age of the Earth. The most obvious constraint is the age of the oldest rocks. These have been dated at up to about four billion years. But actually only a very small portion of the Earth's rocks are that old. From satellite data and other measurements we know that the Earth's surface is constantly rearranging itself little by little as Earthquakes occur. Such rearranging cannot occur without some of the Earth's surface disappearing under other parts of the Earth's surface, re-melting some of the rock. So it appears that none of the rocks have survived from the creation of the Earth without undergoing remelting, metamorphism, or erosion, and all we can say--from this line of evidence--is that the Earth appears to be at least as old as the four billion year old rocks.
When scientists began systematically dating meteorites they learned a very interesting thing: nearly all of the meteorites had practically identical ages, at 4.56 billion years. These meteorites are chips off the asteroids. When the asteroids were formed in space, they cooled relatively quickly (some of them may never have gotten very warm), so all of their rocks were formed within a few million years. The asteroids' rocks have not been remelted ever since, so the ages have generally not been disturbed. Meteorites that show evidence of being from the largest asteroids have slightly younger ages. The moon is larger than the largest asteroid. Most of the rocks we have from the moon do not exceed 4.1 billion years. The samples thought to be the oldest are highly pulverized and difficult to date, though there are a few dates extending all the way to 4.4 to 4.5 billion years. Most scientists think that all the bodies in the solar system were created at about the same time. Evidence from the uranium, thorium, and lead isotopes links the Earth's age with that of the meteorites. This would make the Earth 4.5-4.6 billion years old.
Extinct Radionuclides: The Hourglasses That Ran Out

Figure 6. |
There is another way to determine the age of the Earth. If we see an hourglass whose sand has run out, we know that it was turned over longer ago than the time interval it measures. Similarly, if we find that a radioactive parent was once abundant but has since run out, we know that it too was set longer ago than the time interval it measures. There are in fact many, many more parent isotopes than those listed in Table 1. However, most of them are no longer found naturally on Earth--they have run out. Their half-lives range down to times shorter than we can measure. Every single element has radioisotopes that no longer exist on Earth!
Many people are familiar with a chart of the elements (Fig. 6)
. Nuclear chemists and geologists use a different kind of figure to show all of the isotopes. It is called a chart of the nuclides. Figure 7 shows a portion of this chart. It is basically a plot of the number of protons vs. the number of neutrons for various isotopes. Recall that an element is defined by how many protons it has. Each element can have a number of different isotopes, that is,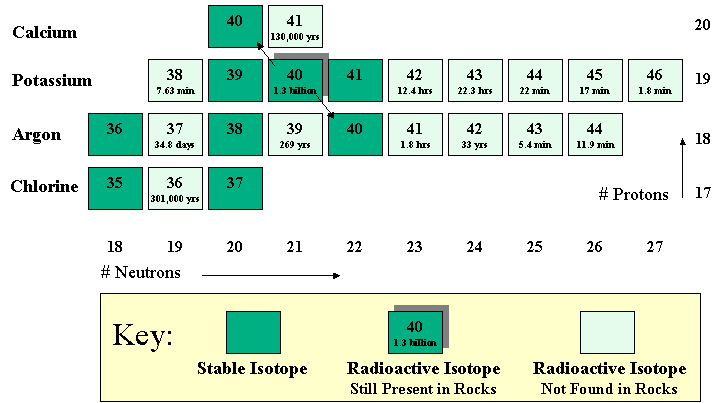
Figure 7. A portion of
the chart of the nuclides showing isotopes of argon and potassium, and
some of the isotopes of chlorine and calcium. Isotopes shown in dark
green are found in rocks. Isotopes shown in light green have short
half-lives, and thus are no longer found in rocks. Short-lived isotopes
can be made for nearly every element in the periodic table, but unless
replenished by cosmic rays or other radioactive isotopes, they no longer
exist in nature. |
atoms with different numbers of neutrons. So each element occupies a single row, while different isotopes of that element lie in different columns. For potassium found in nature, the total neutrons plus protons can add up to 39, 40, or 41. Potassium-39 and -41 are stable, but potassium-40 is unstable, giving us the dating methods discussed above. Besides the stable potassium isotopes and potassium-40, it is possible to produce a number of other potassium isotopes, but, as shown by the half-lives of these isotopes off to the side, they decay away
rather quickly.
Now, if we look at which radioisotopes still exist and which do not, we find a very interesting fact. Nearly all isotopes with half-lives shorter than half a billion years are no longer in existence. For example, although most rocks contain significant amounts of Calcium, the isotope Calcium-41 (half-life 130,000 years does not exist just as potassium-38, -42, -43, etc. do not (Fig. 7). Just about the only radioisotopes found naturally are those with very long half-lives of close to a billion years or longer, as illustrated in the time line in Fig. 8. The only isotopes present with shorter half-lives are those that have a source constantly replenishing them. Chlorine-36 (shown in Fig. 7) is one such "cosmogenic" isotope, as we are about to discuss below. In a number of cases there is
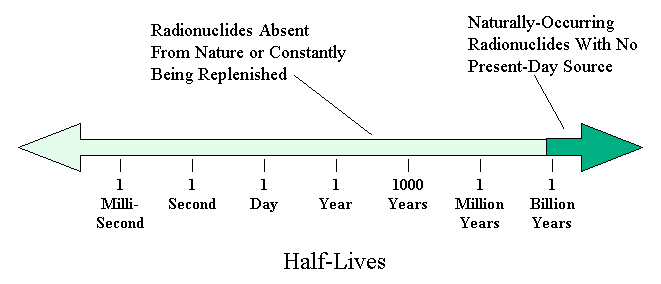 Figure 8. The only naturally-occurring radionuclides that exist with no present-day source have half-lives close to 1 billion years or longer, which still exist from the creation of the Earth. Isotopes with half-lives shorter than that no longer exist in rocks unless they are being replenished by some source. |
evidence, particularly in meteorites, that shorter-lived isotopes existed at some point in the past, but have since become extinct. Some of these isotopes and their half-lives are given in Table II. This is conclusive evidence that the solar system was created longer ago than the span of these half lives! On the other hand, the existence in nature of parent isotopes with half lives around a billion years and longer is strong evidence that the Earth was created not longer ago than several billion years. The Earth is old enough that radioactive isotopes with half-lives less than half a billion years decayed away, but not so old that radioactive isotopes with longer half-lives are gone. This is just like finding hourglasses measuring a long time interval still going, while hourglasses measuring shorter intervals have run out.
Cosmogenic Radionuclides: Carbon-14, Beryllium-10, Chlorine-36
| Table 2.
Extinct
parent isotopes for which there is strong evidence that these once existed in substantial amounts in meteorites, but have since completely decayed away.
|
The last 5 radiometric systems listed up in Table I have far shorter half-lives than all the rest. Unlike the radioactive isotopes discussed above, these isotopes are constantly being replenished in small amounts in one of two ways. The bottom two entries, uranium-234 and thorium-230, are replenished as the long-lived uranium-238 atoms decay. These will be discussed in the next section. The other three, Carbon-14, beryllium-10, and chlorine-36 are produced by cosmic rays--high energy particles and photons in space--as they hit the Earth's upper atmosphere. Very small amounts of each of these isotopes are present in the air we breathe and the water we drink. As a result, living things, both plants and animals, ingest very small amounts of carbon-14, and lake and sea sediments take up small amounts of beryllium-10 and chlorine-36.
The cosmogenic dating clocks work somewhat differently than the others. Carbon-14 in particular is used to date material such as bones, wood, cloth, paper, and other dead tissue from either plants or animals. To a rough approximation, the ratio of carbon-14 to the stable isotopes, carbon-12 and carbon-13, is relatively constant in the atmosphere and living organisms, and has been well calibrated. Once a living thing dies, it no longer takes in carbon from food or air, and the amount of carbon-14 starts to drop with time. How far the carbon-14/carbon-12 ratio has dropped indicates how old the sample is. Since the half-life of carbon-14 is less than 6,000 years, it can only be used for dating material less than about 45,000 years old. Dinosaur bones do not have carbon-14 (unless contaminated), as the dinosaurs became extinct over 60 million years ago. But some other animals that are now extinct, such as North American mammoths, can be dated by carbon-14. Also, some materials from prehistoric times, as well as Biblical events, can be dated by carbon-14.
The carbon-14 dates have been carefully cross-checked with
non-radiometric age indicators. For example growth rings in trees, if counted
carefully, are a reliable way to determine the age of a tree. Each growth ring
only collects carbon from the air and nutrients during the year it is made. To
calibrate carbon-14, one can analyze carbon from the center several rings of a
tree, and then count the rings inward from the living portion to determine the
actual age. This has been done for the "Methuselah of trees", the
bristlecone pine trees, which grow very slowly and live up to 6,000 years.
Scientists have extended this calibration even further. These trees grow in a
very dry region near the California-Nevada border. Dead trees in this dry
climate take many thousands  of years to decay. Growth ring patterns based on wet
and dry years can be correlated between living and long dead trees, extending
the continuous ring count back to 11,800 years ago. "Floating"
records, which are not tied to the present time, exist farther back than this,
but their ages are not known with absolute certainty. An effort is presently
underway to bridge the gaps so as to have a reliable, continuous record
significantly farther back in time. The study of tree rings and the ages they
give is called "dendrochronology".
of years to decay. Growth ring patterns based on wet
and dry years can be correlated between living and long dead trees, extending
the continuous ring count back to 11,800 years ago. "Floating"
records, which are not tied to the present time, exist farther back than this,
but their ages are not known with absolute certainty. An effort is presently
underway to bridge the gaps so as to have a reliable, continuous record
significantly farther back in time. The study of tree rings and the ages they
give is called "dendrochronology".
Calibration of carbon-14 back to almost 50,000 years ago has been done in several ways. One way is to find yearly layers that are produced over longer periods of time than tree rings. In some lakes or bays where underwater sedimentation occurs at a relatively rapid rate, the sediments have seasonal patterns, so each year produces a distinct layer. Such sediment layers are called "varves", and are described in more detail below. Varve layers can be counted just like tree rings. If layers contain dead plant material, they can be used to calibrate the carbon-14 ages.
Another way to calibrate carbon-14 farther back in time is to find recently-formed carbonate deposits and cross-calibrate the carbon-14 in them with another short-lived radioactive isotope. Where do we find recently-formed carbonate deposits? If you have ever taken a tour of a cave and seen water dripping from stalactites on the ceiling to stalagmites on the floor of the cave, you have seen carbonate deposits being formed. Since most cave formations have formed relatively recently, formations such as stalactites and stalagmites have been quite useful in cross-calibrating the carbon-14 record.
What does one find in the calibration of carbon-14 against actual ages? If one predicts a carbon-14 age assuming that the ratio of carbon-14 to carbon-12 in the air has stayed constant, there is a slight error because this ratio has changed slightly. Figure 9 shows that the carbon-14 fraction in the air has decreased over the last 40,000 years by about a factor of two. This is attributed to a strengthening of the Earth's magnetic field during this time. A stronger magnetic field shields the upper atmosphere better from charged cosmic rays, resulting in less carbon-14 production now than in the past. (Changes in the Earth's magnetic field are well documented. Complete reversals of the north and south magnetic poles have occurred many times over geologic history.) A small amount of data beyond 40,000 years (not shown in Fig. 9) suggests that this trend reversed between 40,000 and 50,000 years, with lower carbon-14 to carbon-12 ratios farther back in time, but these data need to be confirmed.
What change does this have on uncalibrated carbon-14 ages? The bottom panel of Figure 9 shows the amount
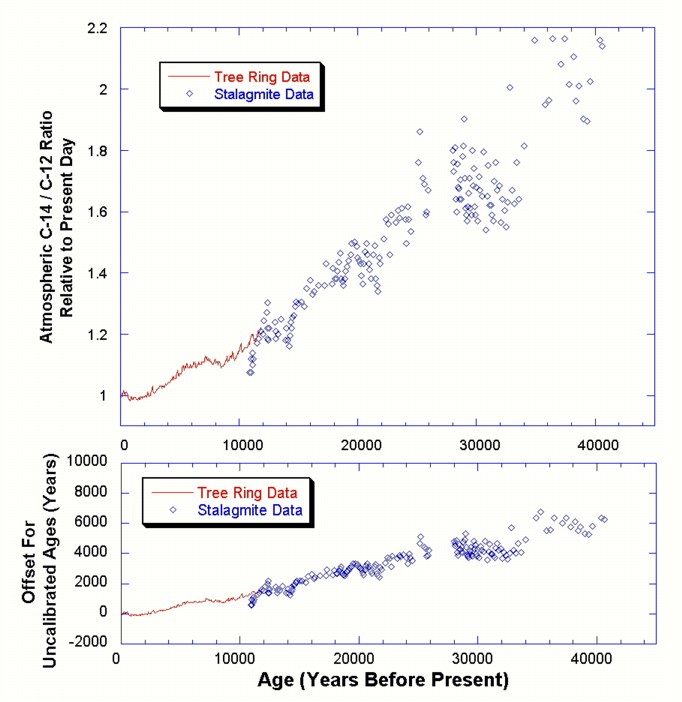
Figure 9. Ratio of
atmospheric carbon-14 to carbon-12, relative to the present-day value
(top panel). Unlike long-term radiometric dating methods, radiocarbon relies on knowing the
fraction of radioactive carbon-14 in the atmosphere at the time the object being dated was alive. The
production of carbon-14 by cosmic rays was up to a factor of about two higher than at present in the timescales
over which radiocarbon can be used. Data
for the last 11,800 years comes from tree-ring counting, while the
data beyond that age comes from other
sources,
such
as from a carbonate stalagmite for the data shown here. The bottom panel
shows the offset in |
of offset in the uncalibrated ages. The offset is generally less than 1500 years over the last 10,000 years, but grows to about 6,000 years at 40,000 years before present. Uncalibrated radiocarbon ages underestimate the actual ages. Note that a factor of two difference in the atmospheric carbon-14 ratio, as shown in the top panel of Figure 9, does not translate to a factor of two offset in the age. Rather, the offset is equal to one half-life, or 5,700 years for carbon-14. This is only about 15% of the age of samples at 40,000 years. The initial portion of the calibration curve in Figure 9 has been widely available and well accepted for some time, so reported radiocarbon dates for ages up to 11,800 years generally give the calibrated ages unless otherwise stated. The calibration curve over the portions extending to 40,000 years is relatively recent, but should become widely adopted as well.
Radiometric Dating of Geologically Young Samples (<100,000 Years)
It is sometimes possible to date geologically young samples using some of the long-lived methods described above. These methods may work on young samples, for example, if there is a relatively high concentration of the parent isotope in the sample. In that case, sufficient daughter isotope amounts are produced in a relatively short time. As an example, an article in Science magazine (vol. 277, pp. 1279-1280, 1997) reports the agreement between the argon-argon method and the actual known age of lava from the famous eruption of Vesuvius in Italy in 79 A.D.
There are other ways to date some geologically young samples. Besides the cosmogenic radionuclides discussed above, there is one other class of short-lived radionuclides on Earth. These are ones produced by decay of the long-lived radionuclides given in the upper part of Table 1. As mentioned in the Uranium-Lead section, uranium does not decay immediately to a stable isotope, but decays through a number of shorter-lived radioisotopes until it ends up as lead. While the uranium-lead system can measure intervals in the millions of years generally without problems from the intermediate isotopes, those intermediate isotopes with the longest half-lives span long enough time intervals for dating events less than several hundred thousand years ago. (Note that these intervals are well under a tenth of a percent of the half-lives of the long-lived parent uranium and thorium isotopes discussed earlier.) Two of the most frequently-used of these "uranium-series" systems are uranium-234 and thorium-230. These are listed as the last two entries in Table 1, and are illustrated in Figure 10.

|
| Figure 10. A schematic representation of the uranium-238 decay chain, showing the longest-lived nuclides. Half-lives are given in each box. Solid arrows represent direct decay, while dashed arrows indicate that there are one or more intermediate decays, with the longest intervening half-life given below the arrow. |
Like carbon-14, the shorter-lived uranium-series isotopes are constantly being replenished, in this case, by decaying uranium-238 supplied to the Earth during its original creation. Following the example of carbon-14, you may guess that one way to use these isotopes for dating is to remove them from their source of replenishment. This starts the dating clock. In carbon-14 this happens when a living thing (like a tree) dies and no longer takes in carbon-14-laden CO2. For the shorter-lived uranium-series radionuclides, there needs to be a physical removal from uranium. The chemistry of uranium and thorium are such that they are in fact easily removed from each other. Uranium tends to stay dissolved in water, but thorium is insoluble in water. So a number of applications of the thorium-230 method are based on this chemical partition between uranium and thorium.
Sediments at the bottom of the ocean have very little uranium relative to the thorium. Because of this, the uranium, and its contribution to the thorium abundance, can in many cases be ignored in sediments. Thorium-230 then behaves similarly to the long-lived parent isotopes we discussed earlier. It acts like a simple parent-daughter system, and it can be used to date sediments.
On the other hand, calcium carbonates produced biologically (such as in corals, shells, teeth, and bones) take in small amounts of uranium, but essentially no thorium (because of its much lower concentrations in the water). This allows the dating of these materials by their lack of thorium. A brand-new coral reef will have essentially no thorium-230. As it ages, some of its uranium decays to thorium-230. While the thorium-230 itself is radioactive, this can be corrected for. The equations are more complex than for the simple systems described earlier, but the uranium-234 / thorium-230 method has been used to date corals now for several decades. Comparison of uranium-234 ages with ages obtained by counting annual growth bands of corals proves that the technique is
highly accurate when properly used (Edwards et al., Earth Planet. Sci. Lett. 90, 371, 1988). The method has also been used to date stalactites and stalagmites from caves, already mentioned in connection with long-term calibration of the radiocarbon method. In fact, tens of thousands of uranium-series dates have been performed on cave formations around the world.
 The uranium-234 / thorium-230 method is now being used to
date animal and human bones and teeth. Previously, dating of anthropology sites
had to rely on dating of geologic layers above and below the artifacts. But with
improvements in this method, it is becoming possible to date the human and
animal remains themselves. Work to date shows that dating of tooth enamel can be
quite reliable. However, dating of bones can be more problematic, as bones are
more susceptible to contamination by the surrounding soils. As with all dating,
the agreement of two or more methods is highly recommended for confirmation of a
measurement. If the samples are beyond the range of radiocarbon (e.g., >
40,000 years), a second method for confirmation of thorium-230 ages may need to
be a non-radiometric method such as ESR or TL, mentioned below.
The uranium-234 / thorium-230 method is now being used to
date animal and human bones and teeth. Previously, dating of anthropology sites
had to rely on dating of geologic layers above and below the artifacts. But with
improvements in this method, it is becoming possible to date the human and
animal remains themselves. Work to date shows that dating of tooth enamel can be
quite reliable. However, dating of bones can be more problematic, as bones are
more susceptible to contamination by the surrounding soils. As with all dating,
the agreement of two or more methods is highly recommended for confirmation of a
measurement. If the samples are beyond the range of radiocarbon (e.g., >
40,000 years), a second method for confirmation of thorium-230 ages may need to
be a non-radiometric method such as ESR or TL, mentioned below.
Non-Radiometric Dating Methods for the Past 100,000 Years
We will digress briefly from radiometric dating to talk about other dating techniques. It is important to understand that a very large number of accurate dates covering the past 100,000 years has been obtained from many other methods besides radiometric dating. We have already mentioned dendrochronology (tree ring dating) above. Dendrochronology is only the tip of the iceberg in terms of non-radiometric dating methods. Here we will look briefly at some other non-radiometric dating techniques.
Ice Cores. One of the best ways to measure farther back in time than tree rings is by using the seasonal variations in polar ice from Greenland and Antarctica. There are a number of differences between snow layers made in winter and those made in spring, summer, and fall. These seasonal layers can be counted just like tree rings. The seasonal differences consist of a) visual differences caused by increased bubbles and larger crystal size from summer ice compared to winter ice, b) dust layers deposited each summer, c) nitric acid concentrations, measured by electrical conductivity of the ice, d) chemistry of contaminants in the ice, and e) seasonal variations in the relative amounts of heavy hydrogen (deuterium) and heavy oxygen (oxygen-18) in the ice. These isotope ratios are sensitive to the temperature at the time they fell as snow from the clouds. The heavy isotope is lower in abundance during the colder winter snows than it is in snow falling in spring and summer. So the yearly layers of ice can be tracked by each of these five different indicators, similar to growth rings on trees. The different types of layers are summarized in Table III.
Ice cores are obtained by drilling very deep holes in the ice caps on Greenland and Antarctica with specialized drilling rigs. As the rigs drill down, the drill bits cut around a portion of the ice, capturing a long undisturbed "core" in the process. These cores are carefully brought back to the surface in sections, where they are catalogued, and taken to research laboratories under refrigeration. A very large amount of work has been done on several deep ice cores up to 9,000 feet in depth. Several hundred thousand measurements are sometimes made for a single technique on a single ice core.
A continuous count of layers exists back as far as 160,000 years. In addition to yearly layering, individual strong events (such as large-scale volcanic eruptions) can be observed and correlated between ice cores. A number of historical eruptions as far back as Vesuvius nearly 2,000 years ago serve as benchmarks with which to determine the accuracy of the yearly layers as far down as around 500 meters. As one goes further down in the ice core, the ice becomes more compacted than near the surface, and individual yearly layers are slightly more difficult to observe. For this reason, there is some uncertainty as one goes back towards 100,000 years. Ages of 40,000 years or less are estimated to be off by 2% at most. Ages of 60,000 years may be off by up to 10%, and the uncertainty rises to 20% for ages of 110,000 years based on direct counting of layers (D. Meese et al., J. Geophys. Res. 102, 26,411, 1997). Recently, absolute ages have been determined to 75,000 years for at least one location using cosmogenic radionuclides chlorine-36 and beryllium-10 (G. Wagner et al., Earth Planet. Sci. Lett. 193, 515, 2001). These agree with the ice flow models and the yearly layer counts. Note that there is no indication anywhere that these ice caps were ever covered by a large body of water, as some people with young-Earth views would expect.
Table III. Polar ice core layers, counting back yearly layers, consist of the following:
|
Visual Layers |
Summer ice has more bubbles and larger crystal sizes |
Observed to 60,000 years ago |
|
Dust Layers |
Measured by laser light scattering; most dust is deposited during spring and summer |
Observed to 160,000 years ago |
|
Layering of Elec-trical Conductivity |
Nitric acid from the stratosphere is deposited in the springtime, and causes a yearly layer in electrical conductivity measurement |
Observed through 60,000 years ago |
|
Contaminant Chemistry Layers |
Soot from summer forest fires, chemistry of dust, occasional volcanic ash |
Observed through 2,000 years; some older eruptions noted |
|
Hydrogen and Oxygen Isotope Layering |
Indicates temperature of precipitation. Heavy isotopes (oxygen-18 and deuterium) are depleted more in winter. |
Yearly layers observed through 1,100 years; Trends observed much farther back in time |
Varves. Another layering technique uses seasonal variations in sedimentary layers deposited underwater. The two requirements for varves to be useful in dating are 1) that sediments vary in character through the seasons to produce a visible yearly pattern, and 2) that the lake bottom not be disturbed after the layers are deposited. These conditions are most often met in small, relatively deep lakes at mid to high latitudes. Shallower lakes typically experience an overturn in which the warmer water sinks to the bottom as winter approaches, but deeper lakes can have persistently thermally stratified (temperature-layered) water masses, leading to less turbulence, and better conditions for varve layers. Varves can be harvested by coring drills, somewhat similar to the harvesting of ice cores discussed above. Overall, many hundreds of lakes have been studied for their varve patterns. Each yearly varve layer consists of a) mineral matter brought in by swollen streams in the spring. b) This gradually gives way to organic particulate matter such as plant fibers, algae, and pollen with fine-grained mineral
matter, consistent with summer and fall deposition. c) With winter ice covering the lake, fine-grained organic matter provides the final part of the yearly layer. Regular sequences of varves have been measured going back to about 35,000 years. The thicknesses of the layers and the types of material in them tells a lot about the climate of the time when the layers were deposited. For example, pollens entrained in the layers can tell what types of plants were growing nearby at a particular time.
Other annual layering methods. Besides tree rings, ice cores, and sediment varves, there are other processes that result in yearly layers that can be counted to determine an age. Annual layering in coral reefs can be used to date sections of coral. Coral generally grows at rates of around 1 cm per year, and these layers are easily visible. As was mentioned in the uranium-series section, the counting of annual coral layers was used to verify the accuracy of the thorium-230 method.
Thermoluminescence. There is a way of dating minerals and pottery that does not rely directly on half-lives. Thermoluminescence dating, or TL dating, uses the fact that radioactive decays cause some electrons in a material to end up stuck in higher-energy orbits. The number of electrons in higher-energy orbits accumulates as a material experiences more natural radioactivity over time. If the material is heated, these electrons can fall back to their original orbits, emitting a very tiny amount of light. If the heating occurs in a laboratory furnace equipped with a very sensitive light detector, this light can be recorded. (The term comes from putting together thermo, meaning heat, and luminescence, meaning to emit light). By comparison of the amount of light emitted with the natural radioactivity rate the sample experienced, the age of the sample can be determined. TL dating can generally be used on samples less than half a million years old. Related techniques include optically stimulated luminescence (OSL), and infrared stimulated luminescence (IRSL). TL dating and its related techniques have been cross calibrated with samples of known historical age and with radiocarbon and thorium dating. While TL dating does not usually pinpoint the age with as great an accuracy as these other conventional radiometric dating, it is most useful for applications such as pottery or fine-grained volcanic dust, where other dating methods do not work as well.
Electron spin resonance (ESR). Also called electron
paramagnetic resonance, ESR dating also relies on the changes in electron orbits
and spins caused by radioactivity over time. However, ESR dating can be
used over longer time periods, up to two million years, and works best on
carbonates, such as in coral reefs and cave deposits. It has also seen
extensive use in dating tooth enamel.
Cosmic-ray exposure dating. This dating method relies on measuring certain isotopes produced by cosmic ray impacts on exposed rock surfaces. Because cosmic rays constantly bombard meteorites flying through space, this method has long been used to date the ' flight time' of meteorites--that is the time from when they were chipped off a larger body (like an asteroid) to the time they land on Earth. The cosmic rays produce small amounts of naturally-rare isotopes such as neon-21 and helium-3, which can be measured in the laboratory. The cosmic-ray exposure ages of meteorites are usually around 10 million years, but can be up to a billion years for some iron meteorites. In the last fifteen years, people have also used cosmic ray exposure ages to date rock surfaces on the Earth. This is much more complicated because the Earth's magnetic field and atmosphere shield us from most of the cosmic rays. Cosmic ray exposure calibrations must take into
account the elevation above sea level because the atmospheric shielding varies with elevation, and must also take into account latitude, as the magnetic shielding varies from the equator to the poles. Nevertheless, terrestrial cosmic-ray exposure dating has been shown to be useful in many cases.
Can We Really Believe the Dating Systems?
We have covered a lot of convincing evidence that the Earth was created a very long time ago. The agreement of many different dating methods, both radiometric and non-radiometric, over hundreds of thousands of samples, is very convincing. Yet, some Christians question whether we can believe something so far back in the past. My answer is that it is similar to believing in other things of the past. It only differs in degree. Why do you believe Abraham Lincoln ever lived? Because it would take an extremely elaborate scheme to make up his existence, including forgeries, fake photos, and many other things, and besides, there is no good reason to simply have made him up. Well, the situation is very similar for the dating of rocks, only we have rock records rather than historical records. Consider the following:
The last three points deserve more attention. Some Christians have argued that something may be slowly changing with time so all the ages look older than they really are. The only two quantities in the exponent of a decay rate equation are the half-life and the time. So for ages to appear longer than actual, all the half-lives would have to be changing in sync with each other. One could consider that time itself was changing if that happened (remember that our clocks are now standardized to atomic clocks!). And such a thing would have to have occurred without our detection in the last hundred years, which is already 5% of the way back to the time
of Christ.
Beyond this, scientists have now used a "time machine" to prove that the half-lives of radioactive species were the same millions of years ago. This time machine does not allow people to actually go back in time, but it does allow scientists to observe ancient events from a long way away. The time machine is called the telescope. Because God's universe is so large, images from distant events take a long time to get to us. Telescopes allow us to see supernovae (exploding stars) at distances so vast that the pictures take hundreds of thousands to millions of years to arrive at the Earth. So the events we see today actually occurred hundreds of thousands to millions of years ago. And what do we see when we look back in time? Much of the light following a supernova blast is powered by newly created radioactive parents. So we observe radiometric decay in the supernova light. The half-lives of decays occurring hundreds of thousands of years ago are thus carefully recorded! These half-lives completely agree with the half-lives measured from decays occurring today. We must conclude that all evidence points towards unchanging radioactive half-lives.
Some individuals have suggested that the speed of light must have been different in the past, and that the starlight has not really taken so long to reach us. However, the astronomical evidence mentioned above also suggests that the speed of light has not changed, or else we would see a significant apparent change in the half-lives of these ancient radioactive decays.
Doubters Still Try
Some doubters have tried to dismiss geologic dating with a sleight of hand by saying that no rocks are completely closed systems (that is, that no rocks are so isolated from their surroundings that they have not lost or gained some of the isotopes used for dating). Speaking from an extreme technical viewpoint this might be true--perhaps 1 atom out of 1,000,000,000,000 of a certain isotope has leaked out of nearly all rocks, but such a change would make an immeasurably small change in the result. The real question to ask is, "is the rock sufficiently close to a closed system that the results will be same as a really closed system?" Since the early 1960s many books have been written on this subject. These books detail experiments showing, for a given dating system, which minerals work all of the time, which minerals work under some certain conditions, and which minerals are likely to lose atoms and give incorrect results. Understanding these conditions is part of the science of geology. Geologists are careful to use the most reliable methods whenever possible, and as discussed above, to test for agreement between different methods.
Some people have tried to defend a young Earth position by saying that the half-lives of radionuclides can in fact be changed, and that this can be done by certain little-understood particles such as neutrinos, muons, or cosmic rays. This is stretching it. While certain particles can cause nuclear changes, they do not change the half-lives. The nuclear changes are well understood and are nearly always very minor in rocks. In fact the main nuclear changes in rocks are the very radioactive decays we are talking about.
There are only three quite technical instances where a half-life changes, and these do not affect the dating methods we have discussed.
1. Only one technical exception occurs under terrestrial conditions, and this is not for an isotope used for dating. According to theory, electron-capture is the most likely type of decay to show changes with pressure or chemical combination, and this should be most pronounced for very light elements. The artificially-produced isotope, beryllium-7 has been shown to change by up to 1.5%, depending on its chemical environment (Earth Planet. Sci. Lett. 171, 325-328, 1999; see also Earth Planet. Sci. Lett. 195, 131-139, 2002). In another experiment, a half-life change of a small fraction of a percent was detected when beryllium-7 was subjected to 270,000 atmospheres of pressure, equivalent to depths greater than 450 miles inside the Earth (Science 181, 1163-1164, 1973). All known rocks, with the possible exception of diamonds, are from much shallower depths. In fact, beryllium-7 is not used for dating rocks, as it has a half-life of only 54 days, and heavier atoms are even less subject to these minute changes, so the dates of rocks made by electron-capture decays would only be off by at most a few hundredths of a percent.
2. Physical conditions at the center of stars or for cosmic rays differ very greatly from anything experienced in rocks on or in the Earth. Yet, self-proclaimed "experts" often confuse these conditions. Cosmic rays are very, very high-energy atomic nuclei flying through space. The electron-capture decay mentioned above does not take place in cosmic rays until they slow down. This is because the fast-moving cosmic ray nuclei do not have electrons surrounding them, which are necessary for this form of decay. Another case is material inside of stars, which is in a plasma state where electrons are not bound to atoms. In the extremely hot stellar environment, a completely different kind of decay can occur. ' Bound-state beta decay' occurs when the nucleus emits an electron into a bound electronic state close to the nucleus. This has been observed for dysprosium-163 and rhenium-187 under very specialized conditions simulating the interior of stars (Phys. Rev. Lett., 69, 2164-2167; Phys. Rev. Lett., 77, 5190-5193, 1996). All normal matter, such as everything on Earth, the Moon, meteorites, etc. has electrons in normal positions, so these instances never apply to rocks, or anything colder than several hundred thousand degrees.
As an example of incorrect application of these conditions to dating, one young-Earth proponent suggested that God used plasma conditions when He created the Earth a few thousand years ago. This writer suggested that the rapid decay rate of rhenium under extreme plasma conditions might explain why rocks give very old ages instead of a young-Earth age. This writer neglected a number of things, including: a) plasmas only affect a few of the dating methods. More importantly, b) rocks and hot gaseous plasmas are completely incompatible forms of matter! The material would have to revert back from the plasma state before it could form rocks. In such a scenario, as the rocks cooled and hardened, their ages would be completely reset to zero as described in previous sections. If this person's scenario were correct, instead of showing old ages, all the rocks should show a uniform ~4,000 year age of creation. That is obviously not what is observed.
3. The last case also involves very fast-moving matter. It has been demonstrated by atomic clocks in very fast spacecraft. These atomic clocks slow down very slightly (only a second or so per year) as predicted by Einstein's theory of relativity. No rocks in our solar system are going fast enough to make a noticeable change in their dates.
These cases are very specialized, and all are well understood. None of these cases alter the dates of rocks either on Earth or other planets in the solar system. The conclusion once again is that half-lives are completely reliable in every context for the dating of rocks on Earth and even on other planets. The Earth and all creation appears to be very ancient.
Apparent Age?
It would not be inconsistent with the scientific evidence to conclude that God made everything relatively recently, but with the appearance of great age, just as Genesis 1 and 2 tell of God making Adam as a fully grown human (which implies the appearance of age). This idea was captured by Phillip Henry Gosse in the book, "Omphalos: An Attempt to Untie the Geological Knot", written just two years before Darwin's "Origin of Species". The idea of a false appearance of great age is a philosophical and theological matter that we won't go into here. The main drawback--and it is a strong one--is that this makes God appear to be a deceiver. However, some
people have no problem with this. Certainly whole civilizations have been incorrect (deceived?) in their scientific and theological ideas in the past. Whatever the philosophical conclusions, it is important to note that an apparent old Earth is consistent with the great amount of scientific evidence.
Rightly Handling the Word of Truth
As Christians it is of great importance that we understand God's word correctly. Yet from the middle ages up until the 1700s people insisted that the Bible taught that the Earth, not the Sun, was the center of the solar system. It wasn't that people just thought it had to be that way; they actually quoted scriptures: "The Earth is firmly fixed; it shall not be moved" (Psalm 104:5), or "the sun stood still" (Joshua 10:13; why should it say the sun stood still if it is the Earth's rotation that causes day and night?), and many other passages. I am afraid the debate over the age of the Earth has many similarities. But I am optimistic. Today there are many Christians who accept the reliability of geologic dating, but do not compromise the spiritual and historical inerrancy of God's word. While a full discussion of Genesis 1 is not given here, references are given below to a few books that deal with that issue.
 As scientists, we deal daily with what God has revealed about
Himself through the created universe. The psalmist marveled at how God, Creator
of the universe, could care about humans: "When I consider Your heavens,
the work of Your fingers, the moon and the stars, which You have set in place,
what is man that You are mindful of him, the son of man that You care for him?"
(Psalm 8:3-4). Near the beginning of the twenty-first century we can marvel all
the more, knowing how vast the universe is, how ancient are the rocks and hills,
and how carefully our environment has been designed. Truly God is more awesome
than we can imagine!
As scientists, we deal daily with what God has revealed about
Himself through the created universe. The psalmist marveled at how God, Creator
of the universe, could care about humans: "When I consider Your heavens,
the work of Your fingers, the moon and the stars, which You have set in place,
what is man that You are mindful of him, the son of man that You care for him?"
(Psalm 8:3-4). Near the beginning of the twenty-first century we can marvel all
the more, knowing how vast the universe is, how ancient are the rocks and hills,
and how carefully our environment has been designed. Truly God is more awesome
than we can imagine!
APPENDIX: Common Misconceptions Regarding Radiometric Dating Methods
There are a number of misconceptions that seem especially prevalent among Christians. Most of these topics are covered in the above discussion, but they are reviewed briefly here for clarity.
1. Radiometric dating is based on index fossils whose dates were assigned long before radioactivity was discovered.
This is not at all true, though it is implied by some young-Earth literature. Radiometric dating is based on the half-lives of the radioactive isotopes. These half-lives have been measured over the last 40-90 years. They are not calibrated by fossils.
2. No one has measured the decay rates directly; we only know them from inference.
Decay rates have been directly measured over the last 40-100 years. In some cases a batch of the pure parent material is weighed and then set aside for a long time and then the resulting daughter material is weighed. In many cases it is easier to detect radioactive decays by the energy burst that each decay gives off. For this a batch of the pure parent material is carefully weighed and then put in front of a Geiger counter or gamma-ray detector. These instruments count the number of decays over a long time.
3. If the half-lives are billions of years, it is impossible to determine them from measuring over just a few years or decades.
The example given in the section titled, "The Radiometric Clocks" shows that an accurate determination of the half-life is easily achieved by direct counting of decays over a decade or shorter. This is because a) all decay curves have exactly the same shape (Fig. 1), differing only in the half-life, and b) trillions of decays can be counted in one year even using only a fraction of a gram of material with a half-life of a billion years. Additionally, lavas of historically known ages have been correctly dated even using methods with long half-lives.
4. The decay rates are poorly known, so the dates are inaccurate.
Most of the decay rates used for dating rocks are known to within two percent. Uncertainties are only slightly higher for rhenium (5%), lutetium (3%), and beryllium (3%), discussed in connection with Table 1. Such small uncertainties are no reason to dismiss radiometric dating. Whether a rock is 100 million years or 102 million years old does not make a great deal of difference.
5. A small error in the half-lives leads to a very large error in the date.
Since exponents are used in the dating equations, it is possible for people to think this might be true, but it is not. If a half-life is off by 2%, it will only lead to a 2% error in the date.
6. Decay rates can be affected by the physical surroundings.
This is not true in the context of dating rocks. Radioactive atoms used for dating have been subjected to extremes of heat, cold, pressure, vacuum, acceleration, and strong chemical reactions far beyond anything experienced by rocks, without any significant change. The only exceptions, which are not relevant to dating rocks, are discussed under the section, "Doubters Still Try", above.
7. A small change in the nuclear forces probably accelerated nuclear clocks during the first day of creation a few thousand years ago, causing the spuriously old radiometric dates of rocks.
Rocks are dated from the time of their formation. For it to have any bearing on the radiometric dates of rocks, such a change of nuclear forces must have occurred after the Earth (and the rocks) were formed. To make the kind of difference suggested by young-Earth proponents, the half-lives must be shortened from several billion years down to several thousand years--a factor of at least a million. But to shorten half-lives by factors of a million would cause large physical changes. As one small example, recall that the Earth is heated substantially by radioactive decay. If that decay is speeded up by a factor of a million or so, the tremendous heat pulse would easily melt the whole Earth, including the rocks in question! No radiometric ages would appear old if this happened.
8. The decay rates might be slowing down over time, leading to incorrect old dates.
There are two ways we know this didn't happen: a) we have checked them out with "time machines", and b) it doesn't make sense mathematically. Both of these points are explained in the section titled, "Can We Really Believe the Dating Systems?"
9. We should measure the "full-life" (the time at which all of the parent is gone) rather than the half-life (the time when half of it is gone).
Unlike sand in an hourglass, which drops at a constant rate independent of how much remains in the top half of the glass, the number of radioactive decays is proportional to the amount of parent remaining. Figure 1 shows how after 2 half-lives, 1/2 x 1/2 = 1/4 is left, and so on. After 10 half-lives there is 2-10 = 0.098% remaining. A half-life is more easy to define than some point at which almost all of the parent is gone. Scientists sometimes instead use the term "mean life", that is, the average life of a parent atom. The mean life is always 1/ln(2) = 1.44 times the half-life. For most of us half-life is easier to understand.
10. To date a rock one must know the original amount of the parent element. But there is no way to measure how much parent element was originally there.
It is very easy to calculate the original parent abundance, but that information is not needed to date the rock. All of the dating schemes work from knowing the present abundances of the parent and daughter isotopes. The original abundance N0, of the parent is simply N0 = N ekt, where N is the present abundance, t is time, and k is a constant related to the half life.
11. There is little or no way to tell how much of the decay product, that is, the daughter isotope, was originally in the rock, leading to anomalously old ages.
A good part of this article is devoted to explaining how one can tell how much of a given element or isotope was originally present. Usually it involves using more than one sample from a given rock. It is done by comparing the ratios of parent and daughter isotopes relative to a stable isotope for samples with different relative amounts of the parent isotope. For example, in the rubidium-strontium method one compares rubidium-87/strontium-86 to strontium-87/strontium-86 for different minerals. From this one can determine how much of the daughter isotope would be present if there had been no parent isotope. This is the same as the initial amount (it would not change if there were no parent isotope to decay). Figures 4 and 5, and the accompanying explanation, tell how this is done most of the time. While this is not absolutely 100% foolproof, comparison of several dating methods will always show whether the given date is reliable.
12. There are only a few different dating methods.
This article has listed and discussed a number of different radiometric dating methods and has also briefly described a number of non-radiometric dating methods. There are actually many more methods out there. Well over forty different radiometric dating methods are in use, and a number of non-radiogenic methods not even mentioned here.
13. "Radiation halos" in rocks prove that the Earth was young.
This refers to tiny halos of crystal damage surrounding spots where radioactive elements are concentrated in certain rocks. Halos thought to be from polonium, a short-lived element produced from the decay of uranium, have been found in some rocks. A plausible explanation for a halo from such a short-lived element is that these were not produced by an initial concentration of the radioactive element. Rather, as water seeped through cracks in the minerals, a chemical change caused newly-formed polonium to drop out of solution at a certain place and almost immediately decay there. A halo would build up over a long period of time even though the center of the halo never contained more than a few atoms of polonium at one time. "Hydrothermal" effects can act in ways that at first seem strange, such as the well-known fact that gold--a chemically un-reactive metal with very low solubilities--is concentrated along quartz veins by the action of water over long periods of time. Other researchers have found halos produced by an indirect radioactive decay effect called hole diffusion, which is an electrical effect in a crystal. These results suggest that the halos in question are not from short-lived isotopes after all.
At any rate, halos from uranium inclusions are far more common. Because of uranium's long half-lives, these halos take at least several hundred million years to form. Because of this, most people agree that halos provide compelling evidence for a very old Earth.
14. A young-Earth research group reported that they sent a rock erupted in 1980 from Mount Saint Helens volcano to a dating lab and got back a potassium-argon age of several million years. This shows we should not trust radiometric dating.
There are indeed ways to "trick" radiometric dating if a single dating method is improperly used on a sample. Anyone can move the hands on a clock and get the wrong time. Likewise, people actively looking for incorrect radiometric dates can in fact get them. Geologists have known for over forty years that the potassium-argon method cannot be used on rocks only twenty to thirty years old. Publicizing this incorrect age as a completely new finding was inappropriate. The reasons are discussed in the Potassium-Argon Dating section above. Be assured that multiple dating methods used together on igneous rocks are almost always correct unless the sample is too difficult to date due to factors such as metamorphism or a large fraction of xenoliths.
15. Low abundances of helium in zircon grains show that these minerals are much younger than radiometric dating suggests.
Zircon grains are important for uranium-thorium-lead dating because they contain abundant uranium and thorium parent isotopes. Helium is also produced from the decay of uranium and thorium. However, as a gas of very small atomic size, helium tends to escape rather easily. Researchers have studied the rates of diffusion of helium from zircons, with the prediction from one study by a young-Earth creationist suggesting that it should be quantitatively retained despite its atomic size. The assumptions of the temperature conditions of the rock over time are most likely unrealistic in this case.
16. The fact that radiogenic helium and argon are still degassing from the Earth's interior prove that the Earth must be young.
The radioactive parent isotopes, uranium and potassium, have very long half-lives, as shown in Table 1. These parents still exist in abundance in the Earth's interior, and are still producing helium and argon. There is also a time lag between the production of the daughter products and their degassing. If the Earth were geologically very young, very little helium and argon would have been produced. One can compare the amount of argon in the atmosphere to what would be expected from decay of potassium over 4.6 billion years, and in fact it is consistent.
17. The waters of Noah's flood could have leached radioactive isotopes out of rocks, disturbing their ages.
This is actually suggested on one website! While water can affect the ability to date rock surfaces or other weathered areas, there is generally no trouble dating interior portions of most rocks from the bottom of lakes, rivers, and oceans. Additionally, if ages were disturbed by leaching, the leaching would affect different isotopes at vastly different rates. Ages determined by different methods would be in violent disagreement. If the flood were global in scope, why then would we have any rocks for which a number of different methods all agree with each other? In fact, close agreement between methods for most samples is a hallmark of radiometric dating.
18. We know the Earth is much younger because of non-radiogenic indicators such as the sedimentation rate of the oceans.
There are a number of parameters which, if extrapolated from the present without taking into account the changes in the Earth over time, would seem to suggest a somewhat younger Earth. These arguments can sound good on a very simple level, but do not hold water when all the factors are considered. Some examples of these categories are the decaying magnetic field (not mentioning the widespread evidence for magnetic reversals), the saltiness of the oceans (not counting sedimentation!), the sedimentation rate of the oceans (not counting Earthquakes and crustal movement, that is, plate tectonics), the relative paucity of meteorites on the Earth's surface (not counting weathering or plate tectonics), the thickness of dust on the moon (without taking into account brecciation over time), the Earth-Moon separation rate (not counting changes in tides and internal forces), etc. While these arguments do not stand up when the complete picture is considered, the case for a very old creation of the Earth fits well in all areas considered.
19. Only atheists and liberals are involved in radiometric dating.
The fact is that there are a number of Bible-believing Christians who are involved in radiometric dating, and who can see its validity firsthand. A great number of other Christians are firmly convinced that radiometric dating shows evidence that God created the Earth billions, not thousands, of years ago.
20. Different dating techniques usually give conflicting results.
This is not true at all. The fact that dating techniques most often agree with each other is why scientists tend to trust them in the first place. Nearly every college and university library in the country has periodicals such as Science, Nature, and specific geology journals that give the results of dating studies. The public is usually welcome to (and should!) browse in these libraries. So the results are not hidden; people can go look at the results for themselves. Over a thousand research papers are published a year on radiometric dating, essentially all in agreement. Besides the scientific periodicals that carry up-to-date research reports, specific suggestions are given below for further reading, both for textbooks, non-classroom books, and web resources.
Resources On the Web:
Virtual Dating--a very helpful educational course on half-lives and radioactive decay was put together by Gary Novak at California State University in Los Angeles. This site has several interactive web "workbooks" to help the reader understand various concepts involved with radiometricdating.
http://vcourseware5.calstatela.edu/VirtualDating
Reasons to Believe--a Christian ministry supporting the old-Earth viewpoint. Dr. Hugh Ross, the founder and head of the ministry, holds a PhD in Astronomy. The ministry supports an accurate interpretation of the Bible while also supportive of science as a tool to study God's creation.
American Scientific Affiliation (ASA)--an umbrella organization of Christians in many different areas of the sciences. Most of the members hold an old-Earth view, though membership is open to anyone supporting their positional statement. This website has numerous resources on theology and Bible-science issues.
Affiliation of Christian Geologists (ACG)--an organization of Geologists who are Christians. The ACG is affiliated with the ASA (above).
Lord I Believe--a site maintained by Hill Roberts, a self-professed conservative Christian and a Physicist. There is a wealth of information, including presentations on the interpretation of Genesis chapters 1-3, a resource list of apologetics ministries, etc.
A review of Phillip Henry Gosse's Omphalos: An Attempt to Untie the Geological Knot, in which fiat creation with the appearance of age is suggested. Reviewed by Rev. John W. Burgeson.
http://www.burgy.50megs.com/omphalos.htm
Origins--this site is devoted mainly to evidences for intelligent design in nature.
Talk Origins--an archive dedicated to creation-evolution issues. Originally created by Chris Stassen, this site is supported by the National Center For Science Education.
A Radiometric Dating Resource List--a very comprehensive resource list for radiometric dating, maintained by Tim Thompson of the NASA Jet Propulsion Laboratory. It includes separate resource sections on the reliability of radiometric dating, introductory articles, advanced articles, radiocarbon dating, etc.
www.geocities.com/CapeCanaveral/8851/radiometric.html
C-14 Dating--The radiocarbon laboratories at Oxford (England) and Waikato (New Zealand) Universities jointly operate this website which gives very comprehensive information on radiocarbon dating. Portions of it were written specifically for use by K-12 students, so it is easy to understand. The site contains explanations on measurements, applications, calibration, publications, and other areas.
Cornell University Geology 656 Lecture Notes--A large number of pdf files of geology lecture notes are available on the web. These are university-level lecture notes describing radiometric dating and related topics.
http://www.geo.cornell.edu/geology/classes/Geo656/656notes98.html
http://www.geo.cornell.edu/geology/classes/Geo656/656notes00.html
Further Reading: Books
Radiometric dating textbooks: The following books are popular college-level Geology texts that deal in depth with various dating techniques. Geologic Time is very easy to read and has been around for quite some time. The text by Dalrymple is meant to be relatively easy to read, but is also very comprehensive. The Faure and Dickin texts are regular textbooks for Geology, including more mathematics and more details.
Dickin, Alan P. (1995) Radiogenic Isotope Geology. Cambridge University Press, 490 pp.
Dalrymple, G. Brent (1991) The Age of the Earth. Stanford University Press, 474 pp.
Faure, Gunter (1991) Principles and Applications of Inorganic Geochemistry: AComprehensive Textbook for Geology Students. MacMillan Pub. Co., New York, 626 pp.
Faure, Gunter (1986) Principles of Isotope Geology, 2nd edition. Wiley, New York, 464 pp.
Eicher, Don L. (1976) Geologic Time, 2nd edition. Prentice-Hall, Englewood Cliffs, NJ, 150 pp.
Other books on dating:
Jespersen, James, and Jane Fitz-Randolph (1996) Mummies, Dinosaurs, Moon Rocks: How We Know How Old Things Are. Atheneum Books, New York, 92 pp.
This is a book designed for easy reading on the general subject of dating. This short book covers topics from archeology to tree ring dating to radiocarbon dating of the dead sea scrolls, to dating of meteorites and moon rocks. The book is out of print, but slightly used copies can be obtained from online dealers like Amazon.
Wagner, G?nther A. (1998) Age Determination of Young Rocks and Artifacts. Springer-Verlag, New York, 466 pp. [Translated from the original Altersbestimmung von jungen Gesteinen und Artefakten, Ferdinand Enke Verlag, Stuttgart, 1995]
This book is a quite comprehensive reference on all methods for determining dates less than about a million years old. It includes a large amount of information on archeological dating, and describes more methods than are discussed here, including TL, ESR, racemization, fluorine/uranium/nitrogen uptake, cosmic-ray exposure-age, fission track, radiocarbon, and others.
Strahler, Arthur N. (1987) Science and Earth History--The Evolution/Creation Controversy. Prometheus Books, Buffalo, 552 pp.
This book is a very thorough and comprehensive refutation of young-Earth ideas, written by a non-Christian. The only negative aspect is that at one point Strahler throws in a bit of his own theology--his arguments against the need for a God. This book is long and in small print; it covers a wealth of information.
For ice core studies, the Journal of Geophysical Research, volume 102, (1997) starting with page 26,315, has 47 papers on two deep ice cores drilled in central Greenland.
Books on scripture, theology, and science:
Snoke, David (1998) A Biblical Case for an Old Earth. Interdisciplinary Biblical Research Institute (IBRI), Hatfield, PA, 76 pp.
Dr. Snoke, an elder in the Presbyterian Church (PCA) and a Physics professor, presents a strong case for a geologically old Earth. He addresses typical objections brought up by young-Earth adherents, including the death of animals before Adam and Eve's sin, entropy (or decay) before the fall, the six days of creation, and the flood.
Sailhamer, John (1996) Genesis Unbound. Multnomah Books, Sisters, OR, 257 pp.
This is a very readable theological book about Genesis. Dr. Sailhamer has served on the translation committees for two versions of the book of Genesis. He has taught at Bethel Seminary, Philadelphia College of the Bible, Trinitiy Evangelical Divinity School, Northwestern College, and Western Seminary.
Ross, Hugh (1994) Creation and Time: A Biblical and Scientific Perspective on the Creation-Date Controversy. NavPress, Colorado Springs, CO.
Hugh Ross has a PhD in Astronomy. In this book Dr. Ross defends modern science and an old age for the universe, and refutes common young-Earth arguments. He firmly believes in the inerrancy of the Bible.
Stoner, Don (1992) A New Look at an Old Earth. Schroeder, Paramount, CA, 191 pp.
A persuasive book written for the Christian layman. Stoner uses arguments both from the theological and the scientific side. He talks somewhat philosophically about whether God deceives us with the Genesis account if the Earth is really old. Stoner also tries to discuss the meaning of the Genesis 1 text.
Van Till Howard J., Young Davis A., and Menninga Clarence (1988) Science Held Hostage. InterVarsity, Downers Grove, IL, 189 pp.
This book talks about the misuse of science by both hard-line atheists and by young-Earth creationists. A good deal of the book is devoted to refuting young-Earth arguments, including a substantial section on the Grand Canyon geology. Its authors are well-known Christians in Geology and Physics.
Wiester, John (1983) The Genesis Connection. Interdisciplinary Biblical Research Institute, Hatfield, PA, 254 pp.
John Wiester has taught Geology at Westmont and Biola University, and is active in the American Scientific Affiliation, an organization of scientists who are Christians. This book discusses many scientific discoveries relating to the age of the Earth and how these fit into the context of Genesis 1.
Young, Davis A. (1982) Christianity and the Age of the Earth. Zondervan, Grand Rapids, MI (now available through Artisan Sales, Thousand Oaks, CA).
Davis Young has a PhD in Geology and teaches at Calvin College. He argues for an old Earth and refutes many of the common young-Earth claims (including their objections to radiometric dating).
Acknowledgements: A number of members of the American Scientific Affiliation and other Christians involved in the sciences reviewed this paper and/or made contributions. The following people are sincerely thanked for their contributions to the first edition: Drs. Jeffery Greenberg and Stephen Moshier (Wheaton College), John Wiester (Westmont College), Dr. Davis Young (Calvin College), Dr. Elaine Kennedy (Loma Linda University), Steven Schimmrich (U. of Illinois), Dr. Kenneth VanDellen (Macomb Community College), Dr. Guillermo Gonzalez (U. Texas, Austin), Ronald Kneusel, and James Gruetzner (U. New Mexico). The second edition, likewise, was significantly improved through reviews by Carol Ann Hill, Hill Roberts, Professor Jeffrey Greenberg (Wheaton College), Ken Wohlgemuth, and Dr. Kenneth Van Dellen. I thank my wife Gwen, and children, Carson and Isaac, for supporting me in this work, and I thank God for giving us the intelligence to understand little bits and pieces of His amazing creation.
More about the author: Dr. Wiens received a bachelor's degree in Physics from Wheaton College and a PhD from the University of Minnesota, doing research on meteorites and moon rocks. He spent two years at Scripps Institution of Oceanography (La Jolla, CA) where he studied isotopes of helium, neon, argon, and nitrogen in terrestrial rocks. He worked seven years in the Geological and Planetary Sciences Division at Caltech, where he continued the study of meteorites and worked for NASA on the feasibility of a space mission to return solar wind samples to Earth for study. Dr. Wiens wrote the first edition of this paper while in Pasadena. In 1997 he joined the Space and Atmospheric Sciences group at Los Alamos National Laboratory, where he has been in charge of building and flying the payload for the solar-wind mission, as well as developing new instruments for other space missions. He has published over twenty scientific research papers and has also published articles in Christian magazines. Dr. Wiens became a Christian at a young age, and has been a member of Mennonite Brethren, General Conference Baptist, and Conservative Congregational, and Vineyard denominations. He does not see a conflict between science in its ideal form (the study of God's handiwork) and the Bible, or between miracles on the one hand, and an old Earth on the other.
GLOSSARY
Alpha decay Radioactive decay in which the atom's nucleus emits an alpha particle. An alpha particle consists of two neutrons and two protons--the same as a helium atom nucleus. In alpha decay, the daughter is four atomic mass units lighter than the parent. Alpha decay is most common in heavy elements.
Atom The smallest unit that materials can be divided into. An atom is about ten billionths of an inch in diameter and consists of a nucleus of nucleons (protons and neutrons) surrounded by electrons.
Beta decay Radioactive decay in which the atom's nucleus emits or captures an electron or positron. The daughter ends up with the same mass as the parent, but ends up with one more neutron and one less proton, or vice versa. Because of the different number of protons, the daughter is a different element with different chemical properties than the parent.
Bound-state beta decay A special kind of beta decay in which an electron is given off by the nucleus, and the electron ends up in an inner orbital, or electron shell. This kind of decay only occurs if the nucleus is stripped of the electrons that would normally be in the inner electron shells. As such, this decay only occurs in the center of stars, and was only confirmed experimentally in the 1990s.
Calibration The cross-checking of one measurement with another, usually more certain measurement. Essentially every method of measurement, whether a thermometer, a ruler, or a more complicated instrument, relies on calibration for accuracy.
Carbonate A term used rather loosely in this context to describe deposits containing the carbonate anion. Carbonates play an important role in many caves, where cave formations are the result of dissolution and re-precipitation of material interacting with carbonic acid. Carbonates in recent cave deposits are useful because of their high carbon content, which can be used to calibrate radiocarbon with uranium-series ages.
Closed system A system (rock, planet, etc.) which has no influence or exchange with the outside world. In reality there is always some exchange or influence, but if this amount is completely insignificant for the process under consideration (e.g., for dating, if the loss or gain of atoms is insignificant) for practical purposes the system can be considered closed.
Cosmic ray A very high-energy particle which flies through space. Cosmic Rays are stopped by the Earth's atmosphere, but in the process, they constantly produce carbon-14, beryllium-10, chlorine-36, and a few other radioactive isotopes in small quantities.
Cosmic-ray exposure dating Dating of surfaces exposed to cosmic rays by measuring the neon-21, helium-3, or other cosmogenic isotopes produced in rocks or meteorites exposed to cosmic rays.
Cosmogenic Produced by bombardment of cosmic rays. Carbon-14 is said to be cosmogenic because it is produced by cosmic rays hitting the Earth's atmosphere.
Daughter The element or isotope which is produced by radioactive decay.
Decay The change from one element or isotope to another. Only certain isotopes decay. The rest are said to be stable.
Dendrochronology The counting of yearly growth rings on trees. A continuous record of growth rings has been used to calibrate radiocarbon ages back as far as 10,000 years ago. "Floating" dendrochronologies (non-continuous records) go back farther in time.
Deposit Mineral or sandy matter settled out of water or accumulated in a vein.
Deuterium 'Heavy hydrogen'; the heavy isotope of hydrogen which contains one proton and one neutron, as compared with only a single proton in normal hydrogen. Water consists of molecules mostly containing normal hydrogen, but with a few molecules containing deuterium.
Electron-capture decay The only type of radioactive decay that requires the presence of something--an electron--outside of the atom's nucleus. Electron capture decay of light atoms--those having the fewest electrons--can be very slightly affected by extremely high pressures or certain chemical bonds, so as to change their half-lives by a fraction of a percent. But no change in the half-lives of elements used for radiometric dating has ever been verified.
Element A substance that has a certain number of protons in the nucleus. Each element has unique properties. Elements may be further broken down into isotopes, which have nearly all of the same properties except for their mass and their radioactive decay characteristics.
Extinct Once in existence, but no longer existing in nature.
Radioactive Subject to change from one element to another. During the change, or decay, energy is released either in the form of light or energetic particles.
Radiocarbon Carbon-14, which is used to date dead plant and animal matter. Radiocarbon is generally not used for dating rocks.
Radiometric dating Determination of a time interval (e.g. the time since formation of a rock) by means of the radioactive decay of its material. Radiometric dating is one subset of the many dating methods used in geology.
Stalactite A cylindrical or conical deposit of minerals, generally calcite or aragonite (forms of calcium carbonate), hanging from the roof of a cavern, and generally formed by precipitation (or crystallization) of carbonates from water dripping from the roof.
Stalagmite Columns or ridges of carbonate rising from a limestone cave floor, and formed by water charged with carbonate dripping from the stalactites above.
Thermoluminescence (TL) dating A method of dating minerals and pottery. Rather than relying on a half-life, this method relies instead on the total amount of radiation experienced by the mineral since the time it was formed. This radiation causes disorder in the crystals, resulting in electrons dwelling in higher orbits than they originally did. When the sample is heated in the laboratory in the presence of a sensitive light detector, these electrons return to their original orbits, emitting light and allowing an age to be determined by comparison of the amount of light to the radioactivity rate experienced by the mineral. Variations on this method include optically-stimulated luminescence (OSL) and infrared-stimulated luminescence (IRSL) dating.
Three-isotope plot In dating, this is a plot in which one axis represents the parent isotope and the other axis represents the daughter isotope. Both parent and daughter isotopes are ratioed to a daughter-element isotope that is not produced by radioactive decay. So the vertical axis gives the daughter/stable ratio while the horizontal axis gives the parent/stable isotope ratio. This type of plot gives the age independent of the original amounts of the isotopes.
Tree ring A ring visible in the sawed or cored section of a tree which indicates how much it grew in a year. The age of a tree can be determined by counting the growth rings.
Two-component mixing The mixing of two different source materials to produce a rock. On rare occasions this can result in an incorrect age for certain methods that use three-isotope plots. Two-component mixing can be recognized if more than one dating method is used, or if surrounding rocks are dated.
Uranium-series decay chain The decay of the long-lived uranium-238 and -235 and thorium-232 which produce shorter-lived radioactive daughters, each of which decay to lighter radioactive elements until they eventually end up as various stable isotopes of lead.
Varve A sedimentary layer showing distinct texture or color for different seasons within a single year. Varve layers can be counted like tree rings.
Xenolith Literally, a foreign chunk of rock within a rock. Some rocks contain pieces of older rocks within them. These pieces were ripped off of the magma chamber in which the main rock formed and were incorporated into the rock without melting. Xenoliths do not occur in most rocks, and they are usually recognizable by eye where they do occur. If unrecognized, they can result in an incorrect date for a rock (the date may be of the older xenolith).