The Science of Thermodynamics:
The Second Law, Entropy, and Evolution
( in Science and in Young-Earth Creationism )
by Craig Rusbult, Ph.D.
Science and Theology
Why is a page about thermodynamics
in a website about origins? Because some young-earth creationists claim
that The Second Law of Thermodynamics makes evolution impossible. This
claim is intended to be partly scientific, because it seems (for those who don't
understand thermodynamics) to be a good argument against evolution, and is partly
theological.
A
condensed introduction to The Second
Law: Entropy and Evolution is available, and I suggest reading it first.
Before it was finished, I wrote the following paragraph as a temporary solution
for the page you're now reading, which is useful for in-depth learning but is
too long for an introduction:
Eventually, I'll write a condensed version
of this page. Until then, if you want "the essential ideas"
you can read the subsections that have a red ball ( •
) at the end of the title and are marked in red
in the Table of Contents and are only 38% of the whole
page. ( You can also read the purple-emphasized
sentences in other subsections. ) / But if you want to understand
thermodynamics and its applications for "origins questions" more thoroughly,
I suggest that you read everything, perhaps by starting with the •-parts
and then reading the whole page.
This is one page in a two-part series about
the science and theology of thermodynamics. You can begin by reading either
page:
•
Science of Thermodynamics (this page) shows that The Second
Law is about mathematical probabilities for energy dispersal, not disorder,
and many common reactions produce a localized decrease of entropy.
•
Theology of Thermodynamics shows that The Second Law is an essential
part of the way God has cleverly designed nature; it is not about sin.
As a scientist, I know thermodynamics well.
I've thought carefully about its application in the area of origins, and I've
asked other scientists to check this page for accuracy.
Why am I writing
these two pages? My motives are similar to those of Allan Harvey,
so I'll just borrow what he says in his page about The
Second Law of Thermodynamics in the Context of the Christian Faith:
My
main purpose here is to dissuade my fellow followers of Christ from pursuing
incorrect arguments based on a lack of understanding of the second law. ...
For those who might find themselves defending the faith to those who are scientifically
literate, I think this is important for three reasons.
The first is that, by abandoning these errors,
we can focus more effectively on legitimate arguments for the faith. ...
The second reason is the special responsibility
to truth we have as people of God. ... We who serve the God of truth should
make a special effort to cleanse our words of all falsehood.
Finally, there is the Christian witness to
the world. ... It is tragic that many think of Christians only as "those
people with the crackpot arguments about a young Earth and entropy" and do not
even consider the Gospel because they think it requires them to believe things
they know to be as silly as a flat Earth. ... This harm to our witness will
only be overcome if Christians... repudiate those arguments (like the misuse
of the 2nd law) that are simply incorrect.
Before moving into
science, here is a brief summary of thermo-theology:
God designed and created the universe so the characteristics
of natural processes would allow life. The Second Law is an essential
part of these cleverly designed characteristics, which allow the reactions that
occur during life, and in sunshine and many other good things in nature.
Although miracles violate the Second Law (since it is an essential part of non-miraculous
natural process), this does not limit divine action because God controls thermodynamics,
not vice-versa.
colors and links: In this page, new concepts
are red, important ideas are purple,
and quotations are dark blue. An
italicized link will keep you inside this
page, but a non-italicized link will open
another page in a new window, so this page remains open in this window.
The
Science of Thermodynamics
1. Entropy
and The Second Law — Entropy is not disorder, and is not always
intuitive; What is entropy and the Second Law? Two
Ways to Increase Entropy; Molecules, Microstates, and Probability;
Disorder is not important in Conventional Thermodynamics, but is very important
in Creationist Thermodynamics.
2. Entropy
and Evolution — Thermodynamics of Evolution
(biological, chemical, and astronomical), Information & Entropy (and
the boy who cried wolf), General Evolution and Fixing
a Four-Alarm Mess.
3A. Why
do things happen? (Part 1) — Two Causes
of Entropy Change (constraint and temperature); Examples of Intuition
(everyday and thermodynamic); What happened? Why did it happen?
3B. Why
do things happen? (Part 2) — A simple reaction in three systems
(isolated, semi-open, and open); In an open system,
is the Second Law always true? Two Reasons (again) for why things
happen. At high temperatures, entropy becomes more important.
4. Why
some things don't happen. — Thermodynamics
and Kinetics; an obstacle that prevents reaction; how
our bodies make unusual things happen; converting
energy into useful functions; Creationist Confusions; Does
life violate the Second Law? The Second Law in Life and Death; Should
we still ask questions?
The red-marked subsections above and the red balls
below (•) are explained earlier.
1. Entropy and the Second
Law
Entropy is not disorder, and is not always
intuitive.
macro and micro: The Second Law of Thermodynamics
can be described in different ways. All of the correct formulations are
technically equivalent, although they can generate different "mental pictures"
about meanings and applications. Some formulations of the Second Law,
at the macroscopic level of everyday objects, use
concepts and illustrations such as energy transfer and steam engines.
( For example, "No process is possible in which the
sole result is the transfer of energy from a cooler to a hotter body."
— from Atkins, 1984 ) But for questions about origins, the most
important applications are at the microscopic level
of molecules and chemistry, so I'll use a formulation that is more useful at
this level, based on statistical mechanics and probabilities.
disorder and intuition: The
correct formulations by scientists (not by writers who are science popularizers)
never say "with time, things become more disordered."
The everyday analogies used by some young-earth creationists — like "a
tidy room becoming messy" due to increasing entropy — are not used
by experts in thermodynamics, because thermodynamics is not about macroscopic
disorder. And these everyday analogies, which depend on human psychological
intuitions about disorder and complexity, are often wrong. No, entropy
is not disorder, and the Second Law is not always
intuitive. But if entropy is not disorder, then what is it?
And what does the Second Law actually say?
What is entropy,
and what is the Second Law?
The modern concept of entropy is based on
quantum mechanics, which states that energy can exist in some amounts but not
others. This quantization of energy is analogous
to the quantization of height when you walk up stairsteps, in contrast with
the continuously variable heights on a smooth ramp. In a system of chemicals,
the total energy of the system is distributed among the many quantized energy
levels in molecules, mainly motional energy
— translational (in moving from one place
to another), vibrational, and rotational
— and (at very high temperatures #) also electronic
energy. In thermodynamics, a system's entropy
is a property that depends on the number of ways
that energy can be distributed among the energy levels of molecules in the system;
entropy is a measure of energy dispersal, of the
extent to which the system's energy is spread out.
Basically,
the Second Law of Thermodynamics is
simple; it says that in every naturally occurring reaction,
whatever is most probable (when all things are considered) is most likely to
happen. #[most likely, or will happen? see appendix]
Of course this is true, but it's trivial until the Second Law defines "most
probable" in terms of "increasing entropy" and claims
that in every naturally occurring reaction, the entropy
of the universe will increase.
Two Ways to increase (or decrease) Entropy •
The Second Law is simple in principle, but applying it
to real systems can be difficult, due to the challenge of "considering
all things" when determining probabilities. During a reaction, the
entropy inside an isolated system will always
increase, and it can increase in two main ways, due to molecule-change or temperature-change:
• Entropy will increase if the amount
of kinetic energy is constant (because the system's mass and temperature are
constant)#[true?] but energy is being dispersed in more ways in the final state
of a system after the molecules (among which energy
is being dispersed) have changed due to the reaction.
• But entropy will also increase if
there is more kinetic energy to be dispersed, and thus more energy-levels that
will be occupied in more ways, even if the molecules don't change. In
this way, a simple increase in temperature (which
is a measure of average kinetic energy) leads to
an increase in entropy, even if there are no other changes in the molecules.
In a system, entropy change can involve only
molecules, only temperature, or both.
The second type of entropy increase, due
to a temperature increase, is especially important for understanding specific
applications of the Second Law because it is a common way to produce a localized
decrease of entropy. This is illustrated with a variety of examples in
Sections 3A and 3B, which explains why things happen.
It's important to notice what the Second
Law does and doesn't say about a reaction: it
does say "the entropy of the universe will always increase",
but it does not say "the entropy of a system
will always increase." There is no guarantee that entropy
will increase in every part of the universe; the entropy of a localized
open system can decrease and it often does decrease,
in reactions that occur both inside and outside living organisms.
Molecules, Microstates,
and Probability
Let's return to the definition of entropy. William
Davies, in an excellent book (Introduction to Chemical Thermodynamics),
shows how entropy is mathematically related to "the
number of microstates corresponding to each distribution, and hence is
[logarithmically] proportional to the probability of each distribution."
Each microstate is a different way to disperse
the same amount of energy in the microscopic realm of atoms and molecules.
Davies explains how the number of microstates — with energy dispersed
in all possible ways throughout the molecules' energy levels — depends
on the properties of molecules, such as the magnitude and spacing of their energy-levels.
He also explains how microstates are related to entropy and to the equilibrium
state that the chemical system will reach after its molecules have finished
reacting. And he describes a useful application of the Second Law:
as a chemical system moves toward its equilibrium state, the number of possible
microstates the system could be in (and still have the same overall macro-state)
will increase with time, because entropy (which depends on the number of
microstates) increases with time, and total entropy (of the universe) is maximum
at equilibrium.
This analogy may help
you understand microstates and probability: Think about the number of
ways that two dice can produce sum-states of 7 (in six ways, 16 25 34 43 52
61) and 2 (in only one way: 11), and why this causes 7 to be more probable than
2. For similar reasons, because of probability, the chemicals in a system
tend to eventually end up in the particular state (their equilibrium state)
that can occur in the greatest number of ways when energy is dispersed among
the zillions of molecules.
Disorder is NOT
important in Conventional Thermodynamics
As emphasized earlier, in a correct formulation
of the Second Law a scientist will never say "things
become more disordered." In a popular thermodynamics website
— it is often cited by other websites (so it's rated #1 by Google) and
it received an Internet Guide Award by Encyclopedia Britannica — Frank
Lambert, a Ph.D. chemist and a teacher whose ideas about entropy have been published
in the Journal of Chemical Education, says: "Discarding
the archaic idea of 'disorder' in regard to entropy is essential. It just
doesn't make scientific sense in the 21st century... [because] it can be so
grievously misleading. ... Judging from comments of leading textbook authors
who have written me, 'disorder' will not be mentioned in general chemistry texts
after the present cycle of editions. {source}"
And in one of my favorite books about chemistry, Introduction to Chemical
Thermodynamics, William Davies (writing in 1972) never mentions "disorder"
in his thorough explanations of energy, entropy, and the Second Law.
If disorder
is not a central concept in thermodynamics, why is it used in some descriptions
of the Second Law? The reasons can be historical, dramatic, epistemological,
or heuristic:
• historical: In the past, scientists
and nonscientists have used "disorder" to describe entropy, so the
inertia of tradition makes it more likely that they will continue to use this
concept now, even though it is not scientifically accurate. { Eventually,
in the appendix I'll write more about this history. }
• dramatic: Part of the problem
is sloppy writing by science popularizers who don't understand the Second Law,
or who have decided that entertaining their readers with colorful everyday analogies
is more important than scientific accuracy.
• epistemological: After explaining
that disorder "is not an axiom or first principle,
and is not derived from any other basic principles," John Pieper
describes disorder in terms of knowledge limitations: "So
in what sense can a system with large entropy be said to be highly disordered?
Just this: the larger entropy is (the more possible microstates there are),
the greater is the uncertainty in what specific microstate will be observed
when we (conceptually) measure at a predetermined moment." (from
Entropy,
Disorder, and Life) #[is this a meaning? the meaning?]
• heuristic: When making a non-mathematical
estimation of entropy changes, the concept of freedom from
constraints (and thus disorder?) is a heuristic device that can often
be useful even though it is not part of the technical definition of entropy.
/ But when using this heuristic, we should remember that: entropy
occurs at the micro-level, so macro-level observations of "disorder"
are usually irrelevant, and so are macro-analogies like "a tidy room becoming
messy"; and entropy change due to a change in constraints is usually
less important than entropy change due to a change in temperature, as you'll
see later in illustrated explanations of "why things happen."
Disorder is VERY important in Creationist
Thermodynamics
Even though "disorder"
is not a central concept in thermodynamics, young-earth creationists imply that
disorder is THE central focus of the Second Law. For example, Henry
Morris stated (in 1976)
that the Second Law "describes a situation of
universally deteriorating order" and it "could
well be stated as follows: In any ordered system, open or closed, there exists
a tendency for that system to decay to a state of disorder."
Morris also illustrates entropy increase
with everyday analogies. For example, in 1973
he quoted Isaac Asimov, a non-creationist writer of popularized science: "The
universe is constantly getting more disorderly! ... We have to work hard to
straighten a room, but left to itself it becomes a mess again very quickly and
very easily. ... How difficult to maintain houses, and machinery, and our own
bodies in perfect working order; how easy to let them deteriorate. In
fact, all we have to do is nothing, and everything deteriorates, collapses,
breaks down, wears out, all by itself and that is what the Second Law is all
about." Although it is true that "we
have to work hard" to maintain order, this has nothing to do with
the Second Law. It would make just as much sense to blame deterioration
on the fact that positive and negative charges attract each other, or any other
basic property of nature. As emphasized above, the Second Law is about
energy states, not messy rooms. If Morris had wanted to correctly describe
the Second Law, he would have been quoting Davies instead of Asimov.
Inspired by Morris, other young-earth creationists
now use everyday examples to mis-illustrate the Second Law. For example,
when Google searches for ["Second Law of Thermodynamics" evolution]
a highly-ranked page is from Christian
Answers Network, and it describes the Second Law as "partially
a universal law of decay; the ultimate cause of why everything ultimately falls
apart and disintegrates over time. Material things are not eternal.
Everything appears to change eventually, and chaos increases. Nothing
stays as fresh as the day one buys it; clothing becomes faded, threadbare, and
ultimately returns to dust. Everything ages and wears out. Even
death is a manifestation of this law. ... Each year, vast sums are spent to
counteract the relentless effects of this law (maintenance, painting, medical
bills, etc.)." This is interesting philosophy, but is sloppy
science, because the Second Law is about energy dispersion, not faded clothing.
2. Entropy and Evolution •
Why are young-earth creationists so excited about thermodynamics?
In 1976, Henry Morris explains his great discovery: "The
most devastating and conclusive argument against evolution is the entropy principle.
This principle (also known as the Second Law of Thermodynamics) implies that,
in the present order of things, evolution in the 'vertical' sense (that is,
from one degree of order and complexity to a higher degree of order and complexity)
is completely impossible. The evolutionary model of origins and development
requires some universal principle which increases order... however the only
naturalistic scientific principle which is known to effect real changes in order
is the Second Law, which describes a situation of universally deteriorating
order." In 1985
he summarizes the logic of his thermo-based argument: "The
law of increasing entropy is a universal law of decreasing complexity, whereas
evolution is supposed to be a universal law of increasing complexity."
Have creationists found a "devastating
and conclusive argument against evolution"? We'll look at
three types of evolution — biological, chemical, and astronomical —
where the answers are NO (but...), and MAYBE, and NO.
Biological Evolution •
Contrary to a common criticism, an evolution
of increasing biological complexity does not violate the Second Law of Thermodynamics.
The Second Law (SL)
is compatible with each of the major actions in neo-Darwinian evolution: mutation
and natural selection. If an overall process of evolution is split into
many small steps involving mutation followed by selection, each step is permitted
by the SL, so the overall process will be SL-permissible.
A neo-Darwinian "one-way ratchet" — with
harmful mutations producing no major permanent change in a population because
organisms with these mutations are eliminated by selection, and rare beneficial
mutations (facilitated by mechanisms such as gene duplication) being preserved
by selection — can produce genetic information and increasingly complex
organisms. Therefore, it's wrong to boldly assert that "it's thermodynamically
impossible for natural evolution to produce an increase in biological complexity."
But when we ask, "What types of complexity can be produced,
in what amounts, and how quickly?", there are reasons to question the plausibility
of an extrapolation from micro-evolution to Total Macro-Evolution. We
should focus our attention on these scientifically important questions instead
of wasting time on unwarranted criticisms that claim the Second Law as justification.
Important questions include rates of change
(in the time available and with reasonable probability, could natural E produce
the changes in DNA that would have been necessary for Total Macro-Evolution?)
and irreducible complexity (do systems exist that
could not have been produced in a process of step-by-step evolution?).
Another page explains principles for a Logical
Evaluation of Evolution and why the scientific support for a natural
"total macro-evolution" is usually overestimated.
Information
and Entropy, and the boy who cried wolf.
When proponents of intelligent
design ask questions about complexity, they often use information
theory to analyze the complexity. Their questions — about
biological evolution and chemical evolution — are worthy of serious consideration,
and scientists are currently debating the merits of their claims.
Information Theory and the Second Law are
both about probabilities, so there may be a connection (in some ways but not
others), and this possibility is discussed in the appendix
where I basically say "I don't know, due to my lack of knowledge about
information theory." But I do know enough to say that questions based
on information theory — about ways to produce complexity, and rates of
its production, and so on — should be disentangled from unwarranted generalizations
about entropy that claim the Second Law as justification. This mixing
causes confusion, and perhaps a "boy who cried wolf" feeling when
unwarranted generalizations about entropy undermine the credibility of scientifically
valid questions about information.
For example, the "four-alarm
mess" described later is illustrated
by the thermodynamics
chapter of the Handy Dandy Evolution Refuter, which combines scientifically
valid ideas — in some good explanations (of thermodynamics and complexity)
and credible arguments (about information and the origin of life, and the biological
value of mechanisms that increase the accuracy of DNA replication) — with
scientific errors and overgeneralizations that are equivalent to crying "wolf"
again and again. For example, the Refuter claims that "local
reversals of natural degeneration (i.e., of entropy increase) can be only very
limited and temporary" [but entropy increase doesn't necessarily
produce macroscopic "degeneration," and
the examples in Section 3A are not "limited and temporary"
unless forming a solar system is "limited" and billions of years is
"temporary"] and "mutations occur according
to the law of increasing entropy (disorder)" [this is true, but
the correct copying of DNA also increases total entropy] and "production
of greater biological complexity by the allegedly natural process of evolution
would, on the other hand, certainly appear to be a violation of the natural
law of degeneration" [no, for reasons explained above].
Chemical Evolution •
As with biological evolution, it is wrong
to assert that a natural production of any complexity is thermodynamically impossible.
But how much complexity can be produced? The origin of life seems to require
a minimal complexity that might be greater than
what can be produced by natural process. Charles Thaxton and Walter Bradley,
in The Mystery of Life's Origin, describe two types of difficulties for
a natural origin of life: chemistry problems, and information problems.
chemistry: In a natural origin of life,
the required chemical reactions — to form organic molecules (amino acids
and nucleotides) that combine into long-chain biomolecules (proteins and RNA)
— are energetically unfavorable, like a ball rolling uphill.
information: A living organism must
have, not just biomolecules, but specific biomolecules that are biologically
useful. For example, if a large number of long-chain proteins did form
(despite the thermodynamically unfavorable chemistry) they would contain a wide
variety of amino acid sequences, and most of these sequences would not produce
useful proteins. Forming a biologically useful protein is extremely improbable,
and Thaxton & Bradley claim that this low probability is equivalent to a
low "configurational" entropy. { How are information and entropy
related? As explained above, I'm not sure. }
There is more about chemical evolution in
the appendix.
Astronomical Evolution •
Most scientists who are Christians are either
evolutionary creationists or old-earth
creationists. We think the universe is 14 billion years old, and
— for reasons outlined below in explanations of "why things happen"
— we accept current scientific theories about the natural development
of stars and galaxies, planets and solar systems, and the atoms that form our
earth and our bodies. But most young-earth creationists
think this astronomical evolution did not occur because the universe
is only about 6000 years old, and it could not occur even in billions
of years because (among other reasons) it would involve "order arising
from disorder" and this would violate the Second Law. / Soon
you'll see examples of astronomical evolution, in Section 3A.
Evolution in General? •
It can be difficult to determine precisely
what young-earth creationists are claiming when they discuss the Second Law,
because different types of evolution often become intertwined in ambiguity,
so it's difficult to know what is being criticized and why. In The
Battle of Beginnings (pages 91-96), Del Ratzsch describes the "four-alarm
mess" involving thermodynamic arguments against evolution —
which are often unclear about what kind of evolution is being criticized; is
it biological, chemical, astronomical, or just evolution in general? —
by major creationists (Henry Morris,...) and by other creationists who borrow
these arguments, plus misunderstandings or misrepresentations by critics of
creationism, and so on.
For example, Henry Morris (in his 1976 paper)
describes all three types of evolution — as indicated in the [square brackets]
below — without making distinctions between them, when he claims that
evolution (E) "requires
some universal principle which increases order, causing random particles eventually
to organize themselves into complex chemicals, non-living systems to become
living cells [chemical E], and populations of worms to evolve into human societies
[biological E]" and he asks, "What is
the information code that tells primeval random particles how to organize themselves
into stars and planets [astronomical E], and what is the conversion mechanism
that transforms amoebas into men [biological E]?"
But it's important to distinguish
between these "evolutions" because they're so different. Section
4 explains why a central scientific claim — that an "energy-converting
mechanism" is necessary to convert raw energy into useful functions —
is relevant for chemical evolution (when the biological mechanisms must be produced)
but is irrelevant for both biological evolution (since by this time the mechanisms
already exist) and astronomical evolution (which is driven by simple attractive
forces, so a mechanism is not needed).
Fixing a Four-Alarm
Mess •
The appendix contains a
review of web-pages by creationists, and I conclude that there is a
wide range of quality, both within pages and between them. Within each
page, valid principles and credible arguments are mixed with scientific errors
and unwarranted generalizations. {an example}
This mixing causes confusion. And it can lead to diminished trust, as
in the story of "the boy who cried wolf," when readers understand
that some of the claims are unwarranted, and then look with suspicion on the
claims that are more scientifically credible. There are also differences
in scientific quality between pages, with the mix-balance (between credible
arguments and unwarranted generalizations) varying from one page to another.
When I first read what Del Ratzsch wrote
about creationist thermodynamics in his excellent book, I told him "you're
being too kind, they're not just confused (and confusing for their readers),
they're wrong." But the more I learn, the more I realize that "four-alarm
mess" is an accurate description. Since young-earth creationists
are mainly responsible for the mess, they should take responsibility for cleaning
it up, for reducing the "cognitive disorder" they have produced.
Here is an overview of what I'm trying to
achieve in this page, in an effort to help reduce the cognitive disorder:
Section 1 explains why "it's not about disorder" and 3A
shows a variety of simple reactions (in the history of astronomical evolution)
in which simple attractive forces produce "increasing order" that
is consistent with the Second Law. Section 3B continues explaining
two factors (constraints and temperature) that determine entropy, in an effort
to replace erroneous "everyday intuitions about entropy" with correct
intuitions based on a correct understanding of entropy. Section 2
(above) makes an urgent plea, to "PLEASE be specific (about the three types
of evolution) when making claims," and this continues in Section 4
which explains why a natural development of "energy-converting mechanisms"
is more relevant, and more challenging, for chemical evolution than for biological
evolution or astronomical evolution.
3A. Why do things happen?
(Part 1) •
This part of the page began earlier when I said "an
increase in temperature leads to an increase in entropy."
A wide variety of common reactions occur when an attractive force brings particles
together, which constrains them (this produces a small decrease of entropy)
but increases their kinetic energy and temperature (this produces a larger increase
of entropy), so total entropy increases even though "disorder" seems
to decrease. We'll analyze some examples from the history of astronomical
evolution — involving three forces (electrical, gravitational, nuclear)
and three particles (electrons, protons, neutrons) — after we look more
closely at the two factors we'll use for the analysis.
Two Causes of Entropy
Change: Constraint and Temperature •
Section 1 described
two types of entropy change: 1) entropy will increase if the amount of
energy is constant but this energy is being dispersed in more ways in the final
state of a system after the particles have changed due to a reaction;
2) entropy will also increase if there is more energy to be dispersed, and thus
more energy-levels that will be occupied in more ways, even if the particles
don't change in any other way.
Soon, we'll look at a variety of important
reactions in the history of nature, will analyze each type of entropy change,
and will ask, "Does overall entropy increase or decrease?" /
1) For the first type of entropy change, a useful principle (but not the only
principle) is to think about constraint change
because when there is more constraint and thus
less freedom of motion, entropy decreases.
For example, entropy decreases when the number of particles decreases (as when
two particles combine to form one particle), or volume decreases (as in compressing
a gas), or in a phase change when particles condense into a more organized form
(as when a gas condenses into a liquid and then into a solid). /
2) For entropy change caused by temperature change,
the principle is simple: when temperature increases, entropy increases.
##[is this "split" valid?]
As you'll see in the examples below, during
a reaction these two factors — constraint and temperature — often
produce opposite effects and are conflicting factors,
with constraint saying "entropy decreases" and temperature saying
"entropy increases." When this happens, usually temperature
increase is the larger factor, so it causes the increase in total entropy for
the universe.
Examples of Intuition: Everyday and
Thermodynamic •
As you'll see in the following examples, much of the astronomical
evolution of our universe is just particles "doing what comes naturally"
when they feel the effect of a force: electrical, gravitational, or nuclear.
When an attractive force pulls particles closer together, thus increasing constraint,
everyday intuition about "disorder" leads
to a conclusion that entropy has decreased, which is wrong. But thermodynamic
intuition, based on a correct understanding of entropy, leads to the
correct conclusion that entropy has increased. Here are some examples,
involving reactions that were important in the early history of nature, and
— because some of them operate in the star that is our sun — in
contemporary history:
• A proton (with positive charge)
and electron (with negative charge) are attracted toward each other due to electrical
force, and eventually — 700,000 years after the Big Bang (according
to a brief history of The
Hot Big Bang) — the temperature is cool enough for them to remain
together and form a hydrogen atom, H. Later, electrical force causes H-atoms
to form HH-molecules: H + H --> HH.
In both reactions — "proton
+ electron --> H-atom" and "H-atom + H-atom --> HH-molecule"
— there are two main factors affecting entropy: 1) the particles'
entropy decreases because the motional freedom of independent particles (which
initially could move around separately) is being constrained (when after the
reaction they must move together as a single unit), but 2) the reaction
"releases" energy which causes an increase of kinetic energy (and
thus temperature) and entropy.
How large are each of these entropy changes?
Using data from a first-year chemistry textbook, it's easy to calculate the
entropy change, DS,
when H-atoms react to form HH-molecules: at the temperature of a warm
room (at 77 Fahrenheit, which is 25 Celsius) the DS
due to constraint-change is -99, and DS
due to temperature-change is +1462, and when these are added we find that total
DS (for the universe) is +1363. {
note: The entropy units are "Joules/Kelvin per mole of HH-molecules formed":
-99 J/K-mol, and so on. }
The direction of these changes (negative
with decrease, or positive with increase) matches our expectations: DS
due to changes of constraint is - (negative) since entropy decreases when two
atoms are constrained into one molecule, DS
due to change of temperature is + (positive) because temperature increases and
when there is more energy there is a wider variety of ways that energy can be
stored in microstates, and DS of
the universe is + (positive) because it must increase during a natural reaction,
as predicted by the Second Law.
What is the change
of system-entropy? This depends on how the system is defined and how "open"
it is to a transfer of energy. As you'll see in Section
3B, if a large amount of energy moves (as heat, photons,...) from the
system to its surroundings, the entropy increase due to temperature-change will
occur in the surroundings, not in the system, and the local system-entropy
can decrease due to its increase of constraints. But in this reaction,
and in those below, there is always an entropy increase for the universe.
• In outer space, HH-molecules are
pulled toward each other by the gravitational force
that produces a mutual attraction between all particles due to their mass.
When the molecules move toward each other they move faster (for the same reason
that a ball rolling downhill moves faster due to the pull of gravitational force)
so their kinetic energy and the overall temperature and entropy increase, even
though the HH-molecules are becoming "clustered together" into a smaller
volume, which constrains them and would seem to decrease their entropy.
• When the temperature is high enough
— several thousand degrees Celsius — both of the HH-forming reactions
(as described above) have been reversed, and the HH-molecules are "jiggled
apart" into protons and electrons. As the compression caused by gravity
continues, the temperature keeps rising and eventually — at 10,000,000
Celsius — the protons are slamming into each other so hard that nuclear
force (which is extremely strong but operates only at very short distances)
overcomes the electrical repulsion between protons; a series of nuclear
reactions begins, and a star is born. The nuclear reactions inside a star
convert some mass into a huge amount of energy (as described by Einstein's "e
= mcc") and even though four protons (with two converted to neutrons) have
been combined into one helium nucleus, so they're highly constrained, energy
from the nuclear reactions increases the temperature so much that the total
entropy increases.
• Eventually, some stars become white
dwarves and then supernovas, and during this process a series of nuclear reactions
produce the heavier elements (lithium,..., carbon, nitrogen, oxygen,..., iron)
that form our planet and our bodies. Again, even though protons and neutrons
are becoming even more constrained within the larger nuclei, the nuclear reactions
liberate a huge amount of energy and this makes the overall entropy change (due
to both constraint-change and temperature-change) is positive, as predicted
by the Second Law.
• When a supernova explodes it ejects
a variety of heavy-nucleus atoms into space where, due to gravitational attractions,
they can eventually condense into planets that (due to gravitational attraction)
form solar systems. #[true?]
Many other reactions also occurred while
the universe was developing, but these reactions are omitted here because my
goal is to illustrate the Second Law, not to describe a comprehensive history
of nature.
What happened? •
The overall result of these reactions —
which produce hydrogen atoms and molecules, stars, heavy-nucleus atoms, planets,
and solar systems — is an "astronomical evolution" that produces
a change from simplicity to complexity, and an increase in ordered structures
at the microscopic and macroscopic levels. But the Second Law doesn't
claim that increased complexity is impossible. None of these reactions
violates the Second Law, and neither does the overall process.
While these localized reactions were happening,
an overall mega-reaction of the universe was its expansion from an ultra-dense
beginning into a much larger volume, which produced a large decrease in constraints
and a large increase of entropy. Allan Harvey says, of this expansion,
that "astrophysicists, using data such as the cosmic
background radiation, have verified that the universe has obeyed the second
law of thermodynamics very well since the time of the big bang. The 2nd
law predicts that something small and hot should become larger and colder, and
that is just what has happened. (source)"
Yes, the small-scale localized contractions (which
were due to attractive forces, with entropy increasing due to a temperature
increase) and the larger-scale overall expansion
(which occurred for other reasons, with entropy increasing due to a decrease
of constraint) both produced an increase of total entropy in the universe. #[astro,
local decreases also increase overall S?]
Why did it happen?
a review: For each reaction, the
main principles for "why it happened" are explained earlier:
overall entropy-change is caused by two factors, with constraint-changes usually
being less important than temperature-change.
a preview: The rest of Section 3A
is a brief summary, comments about intuition, and another perspective.
a summary: In each reaction, attractive
forces pull particles closer together (thus increasing constraints and decreasing
apparent disorder) but this increases the particles' kinetic energy (and thus
their temperature and entropy) and overall entropy increases, consistent with
the Second Law.
unhelpful intuition: For these reactions
and many others, everyday intuitions about "entropy as disorder" lead
to conclusions that are wrong. With psychological intuitions about disorder,
the main difficulty is that temperature-change is being ignored even though
it usually determines the overall entropy-change.
helpful intuition: Usually, it's
better to think about the attractive forces (electrical, gravitational, or nuclear)
acting on particles, and simply conclude that if particles are "doing what
comes naturally" then the Second Law is being obeyed.
Another Perspective on The Second Law
Why did it happen? When attractive
force (or repulsive force) makes particles "do what comes naturally"
in a reaction — like balls rolling downhill — some potential
energy (*) is converted into kinetic
energy. In each example above, this additional kinetic energy is
the "temperature factor" that causes an increase of total entropy.
The total energy remains constant (this conservation of
energy is The First Law of Thermodynamics)
but after the potential-to-kinetic conversion less of the total energy is capable
of doing work. This loss of "energy that can do work" is described
in another formulation of The Second Law: "Every
naturally occurring transformation of energy is accompanied, somewhere, by a
loss in the availability of energy for the future performance of work."
{ R. B. Lindsay, American Scientist (1959), p 378. }
* potential
energy depends on position: For example, when far-apart particles with
opposite charge (like positive protons and negative electrons) move toward each
other because they are mutually attracted by electrical force, they become close-together
particles. In this reaction, their positions have changed from far apart
(with relatively high potential energy) to closer together (with lower potential
energy) and part of their potential energy (which is potentially capable
of doing work when it is converted into kinetic energy) already has
been converted into kinetic energy, and this part of the energy cannot "do
it again" and is therefore not available "for
the future performance of work." Similarly, water at the top
of a dam has high gravitational potential energy, and gasoline has high
chemical potential energy, because each has the potential for doing work
— when the water falls to a lower height, or the gasoline reacts (with
oxygen) to form stable chemicals that have lower potential energy.
3B.
Why do things happen? (Part 2)
This section continues the explanation of "why things
happen" that began in Part 1. It explains
how to think about the Second Law — and the two factors that produce entropy
change — in systems that are open or closed (in which energy can or cannot
move across the system's boundaries) and provides another illustration of why
everyday intuitions about "entropy as disorder" are often wrong.
We'll carefully examine a simple example in two stages, for three types of systems:
isolated, semi-open, and open.
First, however, here
is a brief preview/summary of Section 3B:
For a simple reaction
in which three gas molecules (HH OO HH) become two liquid molecules (HOH HOH),
what are the changes of entropy?
In a system that is isolated,
the entropy changes are analogous to the reaction-changes in Section
3A: during the reaction that forms HOH, the constraint-changes
(with three molecules becoming two, and gas becoming liquid, *)
produce a small entropy decrease, but temperature-change (during the explosive
reaction) produces a larger entropy increase, so entropy increases inside the
isolated system, which is thermodynamically equivalent to a miniature universe.
/ * Other entropy-determining characteristics
(molecular energy levels,...) also differ for the initial and final molecules,
but the two major constraint-changes are 3-to-2 and gas-to-liquid.
In a system that is semi-open,
if kinetic energy escapes from the system (into the surroundings) as heat and
the system's initial and final temperatures are the same, now (in contrast with
the isolated system) there is no entropy increase due to temperature-change
(because the temperature doesn't change), but entropy is lost due to constraint-changes,
so entropy of the system decreases by a small amount.
But the surroundings gains kinetic energy and its
entropy increases by a larger amount, so for the universe
(= system + surroundings) entropy increases.
What is a "small amount" and
"larger amount"? For this reaction, here are the relative size
of three entropy changes: -327 (decrease for the system due to
constraint-changes), +1917 (increase for the surroundings due to temperature-change,
which occurs because electrical "chemical bonding" has become stronger
during the reaction), and these combine to give +1590 (increase for the universe).
{ This section also shows another formulation of the Second Law, which is used
in most first-year chemistry textbooks: "DH
(of system) - T DS (of system) = DG
(of system)" and DG (of system) decreases in
a reaction. }
At normal temperatures these sizes are
typical, because most chemical reactions are "driven forward" by an
increase in bond strength, not by a decrease in constraints. But entropy
becomes more important as temperature increases, which is why water forms ice
(with strong bonds) at low temperatures, or gas (with minimal constraints) at
high temperatures, or liquid (a compromise between strong bonds and minimal
constraints) at in-between temperatures.
Now, here is a more
thorough analysis:
An Isolated System (with a simple
reaction)
Imagine that a system containing 2 trillion
molecules of hydrogen (HH) and 1 trillion molecules of oxygen (OO) is "closed"
to prevent both matter and energy from entering or escaping. This isolated
system is thermodynamically equivalent to a miniature universe, so the
Second Law predicts that in any natural reaction the entropy of this isolated
system (the mini-universe) will increase.
Now imagine that the chemicals react explosively
to form water, in the reaction "HH + OO + HH --> HOH + HOH", which
can also be written as "2 H2 (gas) + O2 (gas) -->
H2O (liquid)".
During this reaction, there are two causes
of entropy change, involving constraints and temperature: 1) The
atoms are more constrained when, instead of moving around in 3 trillion
small molecules (at the start) they are constrained in only 2 trillion larger
molecules (at the end), and instead of gases (HH and OO) the product is a liquid
(HOH); these constraint-factors (*)
produce a small decrease in entropy. 2) But the system's temperature increases
— which occurs because the atoms have formed stronger
bonds (i.e., the chemical bonds are stronger in HOH than they were in
HH and OO, due to changes in the strength of electrical attractions and repulsions)
— and this temperature-factor causes a large
increase of entropy.
When these two factors are combined, the
overall entropy of the system increases, as predicted by the Second Law.
For this situation, everyday intuition about "disorder" is wrong because
it includes only the constraint-factor, and it ignores the temperature-factor
that in this reaction (and most other reactions) actually determines whether
the total universe-entropy increases.
* Other
constraint-changes also occur, because other entropy-determining characteristics
(molecular energy levels,...) are different for the initial and final molecules,
but these changes are smaller than the major constraint-changes described above:
3 molecules change to 2 molecules, and gases change to liquid.
A Semi-Open System (with the same
simple reaction)
Imagine a system like the one above, but
now instead of being closed it is semi-open so
there can be a transfer of energy but not a transfer of matter. How?
The HH and OO are in a metal tank that is surrounded by a large tub of water,
and heat energy can transfer between the tank and tub, which begin at the same
temperature. After the explosive chemical reaction, the temperature inside
the tank initially increases a lot, but then heat energy transfers out of the
tank (moving from high temperature to low temperature) until the tank and tub
are at the same temperature. We'll imagine that the tub of water is huge,
so its change of temperature will be very small, and it's a good approximation
to consider the system's initial and final temperatures to be the same.
Here are the entropy changes for the system
and its surroundings, and for "system plus
surroundings" which is the universe:
The system is open to energy transfer, so
it loses energy to the huge tub of water, and the system's initial and final
temperatures are almost the same; the increase of system-entropy due to
temperature increase is extremely small, and it can be ignored. Therefore,
the system's change of entropy is determined only by changes in the entropy-determining
characteristics of the initial and final molecules (HH-and-OO versus HOH);
the most important of these molecular changes — a decrease in the number
of molecules, and a change from gas to liquid — increase constraint, so
the system's entropy decreases.
Outside the tank, in the tub of water, the
molecules don't change (they begin and end as HOH) so there is only one factor:
the water temperature has increased slightly, so the entropy of the tub-water
(the surroundings) has increased. / You may have noticed a logical
inconsistency in this analysis, so I'll explain why it is numerically acceptable.
The temperature increase is very small for both the system and its surroundings,
but there is a major difference — the system contains a small amount of
matter, while the surroundings contains a HUGE amount of matter — so the
temperature-caused entropy increase is negligible for the system (because small
x small = small) but is significant for the surroundings (because small x huge
= large).
Overall, when we add the entropy change inside
the system (in the tank where entropy decreases) and outside the system (in
the surroundings, in the tub-water where entropy increases) we find that the
overall entropy of the universe (system + surroundings) has increased,
as predicted by the Second Law, even though the entropy of the system
has decreased.
An Open System (with the same simple
reaction)
Imagine a system that, instead of being semi-open
(with a transfer of energy but not matter), is open
(with a transfer of both energy and matter). Now imagine that the same
reaction occurs, as in the semi-open system above, but then 25% of the products
(the HOH formed in the reaction) escape from the system. Because this
25% of the HOH carries away 25% of the system's microstates
(its ability to disperse energy in different ways) the system's entropy decreases
by 25%, to 75% of its original value. But the surroundings gains entropy
from the escaped HOH, and the total entropy of the universe still increases.
Of course, the surroundings also gain energy
from the escaping HOH. Because a transfer of matter automatically involves
a transfer of energy, a logically possible type of system (with a transfer of
matter but not energy) never occurs in reality, so this possibility is ignored
in thermodynamics.
Applications of the Second Law are similar
for systems that are semi-open and open. In either type of system, when
energy leaves the system (or enters it), some (or all) of the entropy change
that is associated with a change of kinetic energy (and change of temperature)
is transferred to the surroundings.
In
an open system, is the Second Law always true? •
Yes. As stated in the Second Law, entropy
of the universe always increases when a reaction occurs.
The entropy of an isolated system (with no transfer of matter
or energy) always increases, because this closed system is thermodynamically
equivalent to a miniature universe. But during a reaction the
entropy of a system that transfers energy (an open system or
semi-open system) can increase, decrease, or stay constant.
Sometimes you'll see a claim that "the
Second Law does not apply to an open system," but this is wrong.
An incorrectly stated Second Law — claiming that "entropy [of
a system] always increases" — does not apply to an open (or semi-open)
system. But the correct Second Law —
claiming that "entropy of the universe always increases —
does apply to every system, whether it is isolated, semi-open,
or open.
In an open system, is the system's entropy
important? •
Occasionally. At normal temperatures,
most reactions are "driven forward" by the action of forces that lead
to the formation of stronger attractive interactions between particles, and
changes in system-entropy are not very important. But system-entropy is
always important in some systems [#examples?]
and it always becomes more important at high temperatures.
Although "applications
of the Second Law are similar for systems that are semi-open and open,"
the details of application are more complicated for an open system, so the following
analysis will be done for a semi-open system.
Two Reasons
(again) for "why things happen"
It is easier to understand what happens inside a semi-open
system, and why it happens, if we use another formulation of the Second Law
(*), DH
- T DS = DG,
where "D"
means "change", and DH
is the energy-change of a system due to the heat-energy it absorbs (usually
this is due to changes in the strength of chemical bonding), T
is the system's temperature (which is assumed to be the same before and
after the reaction), DS
is the change in the system's entropy, and DG
is the change in the system's free energy.
Notice that every term is for the system, which makes it easier for scientists
to focus their attention on their interest, which is the system.
The Second Law states that in a naturally occurring reaction
the system's FREE ENERGY decreases, which occurs when the universe's
ENTROPY increases.
In a formulation of the Second Law as "+DH
-TDS = DG" we can
clearly see that two factors (+DH and -TDS)
determine whether DG is negative (so the reaction
is thermodynamically favorable and it could occur) or positive (so the reaction
is unfavorable and it will not occur). These two factors, involving the
systems's energy change (DH) and the
system's entropy change (DS), are equivalent
to the temperature-factor and constraint-factor,
respectively, that were used to analyze entropy in the examples above, to illustrate
why things happen.
It's important to recognize that two factors
determine a change in universe-entropy. But young-earth creationists usually
ignore the important difference between universe-entropy and system-entropy,
which is equivalent to ignoring the existence of two factors in "+DH
-TDS". They focus on system-entropy (DS)
even though -TDS is usually the less important factor
because at normal temperatures most chemical reactions
are "driven forward" by the formation of stronger bonds (DH),
not by an increase of the system's entropy (DS).
* This
DG-formulation
of the Second Law, DH - T
DS = DG, is equivalent to the conventional
Second Law (described in terms of entropy) that is used throughout this page.
It's easy to begin with a DS-formulation
of the Second Law, "DS
(of surroundings) + DS (of system) = DS
(of universe)" with DS (of universe) increasing
in a reaction, and mathematically derive the DG-formulation,
"DH (of system) - T
DS (of system) = DG (of system)" with
DG (of system) decreasing in a reaction.
This derivation is explained in most introductory first-year chemistry books,
which use "DH - T DS
= DG" to analyze changes of energy and entropy
in chemical reactions. With proper modifications, this DG-formulation
can be used to analyze and understand all reactions, not just chemical reactions.
note: If you're
bothered (or bored) by numbers, you can skim for awhile (absorbing what you
can but not getting bogged down in details) until you reach the important principle
in the final paragraph: "We can see that the reaction
occurs... because..."
Using data from the appendix of a first-year
chemistry textbook (Chemistry and Chemical Reactivity, by Kotz &
Treichel, 5th Edn, 2003), I calculated the standard values
of DH, -TDS, and DG
for the water-forming reaction above, and then multiplied each term by "-1/T"
to convert these back into the corresponding terms in the DS-formulation
of the Second Law. For the reaction of "2 moles HH (gas) + 1 mole
OO (gas) --> 2 moles HOH (liquid)" we find that, with entropy measured
in units of joules/Kelvin, and energy in kilojoules,
DS of the surroundings
is +1917, because DH of the system is -571
;
DS of the system
is -327, because -TDS of the system is +97
; and
DS of the universe
is +1590, because DG of the system is -474
.
We can see that
the reaction occurs (consistent with the Second Law, since DS
of the universe increases, with DS of universe =
+1590 J/K) because the favorable increase in bond strength
(which produces DH = -571 kJ, and DS
of surroundings = +1917 J/K) is more important than
the unfavorable increase in molecular constraints (which produces
-TDS = +97 kJ, and DS
of system = -327 J/K).
Here is another water-example to illustrate
the two factors:
While you're reading this, your body contains two phases
of water — liquid and gas. Why?
Basically, it's due to "the two factors"
in action, as described above and below. A system's tendency to form
STRONGER BONDS (which shows up in the system's energy factor,
DH) favors liquid-HOH, while a system's tendency
to attain HIGHER PROBABILITY (which shows up in the system's entropy
factor, TDS) favors gas-HOH.
It's easy to understand why bonds between
HOH neighbors are stronger in liquid (where HOH-neighbors are close together,
within "touching" distance) than in gas (where HOH-neighbors are far
apart, isolated from each other).
To understand why gas has a higher probability,
imagine a small cup of water in a large room. If all other things were
equal (with no forces between HOH-neighbors) the HOH molecules would be evenly
spread throughout the entire room, and very few HOH molecules would be in the
cup as liquid-water, instead most would be outside the cup as gas-water.
But even though it's very improbable that
most molecules would be in the small cup, under some conditions this does occur
(whenever you see water in a cup) due to STRONGER BONDS, while in other conditions
all of the water evaporates (so the cup is empty and dry) due to HIGHER PROBABILITY.
note: This analysis-and-explanation
is correct but is incomplete, since it doesn't include relevant factors like
rates of reaction (for evaporation and condensation), dynamic equilibrium, relative
humidity, and so on.
At high
temperatures, entropy becomes more important.
For every reaction, in any type of system,
entropy of the universe always increases. But the entropy of a
system does not always increase.
Usually, chemical reactions occur due to
a formation of stronger bonds (DH), not an increase
of system-entropy (DS). But the whole factor
is "- T DS" so this factor becomes
more important as temperature increases, and system-entropy is always the determining
factor at high temperatures. What is a high temperature? It depends
on the reaction, so "high temperature" differs for the melting of
ice (when a "high T" is 274 Kelvin) and the melting of table salt
(when a "high T" is 1075 Kelvin).
Consider three phases of H2O —
solid, liquid, and gas at a pressure of 1 atmosphere — in three ranges
of temperature: • Scientists have observed that at low temperatures
(below 0 Celsius, which is 273 Kelvin, or 32 Fahrenheit) the DH
(with strong bonds) is most important; because ice has the strongest bonds,
at "T = -1 Celsius" the most stable form of HOH is solid ice.
• But the entropy term is "- T DS"
and at high temperatures (above 100 C, or 373 K, or 212 F) the DS
(with minimal constraints) is most important; because gas has the smallest
constraints, at 101 Celsius the most stable form of HOH is the gas, water vapor.
• At intermediate temperatures, between 1 C and 99 C, the most
stable form of HOH is liquid water. / At the melting point or boiling
point, at 0 C or (if pressure = 1 atmosphere) 100 C, respectively, two phases
(solid and liquid, or liquid and gas) are equally stable. { Details about
what happens at 0 C and 100 C, explained using the concepts of irreversible
reaction and reversible reaction, are in
the appendix. }
4. Why some things
don't happen,
and how our bodies can
"make unusual things happen."
Thermodynamics and Kinetics •
If we think of all possible reactions, and ask "Why
do some reactions occur, but others don't occur?", we find two reasons:
thermodynamic and kinetic. In thermodynamics,
we ask "is a reaction thermodynamically favorable?" In kinetics,
we ask "if a reaction can occur, when will it occur and how quickly?"
So far in this page, we've looked at only thermodynamics. But there is
a hint of kinetics in Section 1 where I waffle by
saying that chemicals "tend to eventually end
up in their equilibrium state" instead of just saying they "will
end up..."?
Why is it wise to waffle when making thermodynamic
claims? Because the principles of thermodynamics let us predict whether
a reaction can occur, and what the equilibrium state would be if it does
occur, but thermodynamics does not say when it will occur (and whether
it will probably occur in a given amount of time), or how quickly.
To help us answer these questions, we can use our observations of "what
does and doesn't happen" plus the principles of kinetics.
As contrasting examples of "how quickly,"
the reactions of oxygen with iron and with gasoline are both thermodynamically
favorable, but the oxidation of iron occurs slowly (in rusting) while the oxidation
of gasoline occurs quickly (in a fire).
An
Obstacle that Prevents Reaction •
The question, "How quickly?", can
be answered in two ways because "quickly" has two meanings.
The kinetic answer above, re: slow rusting or fast burning, is about speed
of reaction. Another kinetic answer is about the timing
of reaction, and a more precise question is, "When will a reaction
occur?"
Gasoline can exist in a car's gas tank for
years without reacting, so during this time it is not reacting quickly.
But when we start the car's engine, a spark initiates a reaction which is so
fast that it becomes a small-scale explosion when the gases produced by the
reaction are confined within a cylinder of the engine. Why can the reactive
chemicals (gasoline and oxygen) exist for years without reacting? Because
the chemicals must overcome an obstacle — an "activation energy"
— before the fast reaction can occur.
What is activation energy? To illustrate
by analogy, imagine a red ball that is trapped in a transparent bowl on top
of a green hill.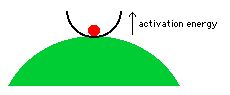 
The ball is thermodynamically unstable because
it would roll down the hill if it could. But this thermodynamically favorable
reaction will occur only if the ball can first escape from the bowl. The
action of the ball climbing up and over the bowl's edge is analogous to chemicals
overcoming their activation energy. Until this occurs, the ball is in
a metastable state; it is temporarily stable, even
though it would react (by rolling down the hill) if it could. Similarly,
the gasoline and oxygen would react, but they don't react until the spark allows
some of the molecules to overcome their activation energy; this lets them
react and they "release energy" to their neighbors, which lets these
neighbors overcome their activation energy so they can react and release energy
to their neighbors, and so on, in a self-sustaining chain reaction that occurs
very quickly, after it begins.
As with most things in nature, the results
of activation energies can be either bad or good. We want some reactions
to occur, but they don't occur due to activation energies, and this is bad.
But gasoline doesn't burn in a car's gas tank, only in the engine, and this
is good. Activation energies are also biologically useful because they
provide a kinetic obstacle — so undesirable reactions are prevented, and
(as explained below) desirable reactions can be controlled — and this
allows life.
How our bodies make
unusual things happen. •
Inside our bodies, reactions occur that would
not occur outside our bodies, and molecules exist that would not exist outside
our bodies. How and why can this happen?
kinetics: Many reactions that usually
are kinetically unfavorable can occur because some proteins,
which are called enzymes, act as catalysts
that "make things happen" by providing a way to lower the activation
energy and/or bring chemicals together in a spatial orientation that is "just
right" for reacting. Enzymes operate in the context of control
systems that control which reactions do and don't occur, and when.
These control systems are analogous to a thermostat that turns a furnace on
and off, when we do and don't need heat, but are much more complex and wonderful.
thermodynamics: Many reactions that
usually are thermodynamically unfavorable can occur when they are part of a
coupled reaction. For example, if a biologically useful reaction that
is unfavorable (because it produces a change of -400 in universe-entropy) is
combined with a sufficiently favorable reaction (that produces a change of +500
in universe-entropy) the overall coupled reaction
is favorable, since it produces an increase of +100 in universe-entropy.
Our bodies use external fuel (with chemical potential energy stored in the foods
we eat and the oxygen we breathe) to produce internal fuel (with energy temporarily
stored in "high energy" molecules such as adenosine triphosphate,
ATP) that is used in coupled reactions.
Converting Energy into Useful Functions •
The overall result of biochemistry
(the chemistry that occurs inside our bodies) is to produce a "living environment"
with molecules and reactions that would not occur outside our bodies.
This is a metastable environment, with high energy and low entropy, that is
maintained by the use of external energy. In a book about The Mystery
of Life's Origin, Chapter 7 (the
first chapter about thermodynamics) explains how living organisms can exist
despite their unfavorable energy and entropy, by converting external energy
into useful internal functions. Here is my brief summary:
Localized areas of high entropy can be maintained
by a flow of energy. For example, if electrical energy flows through water,
HH will form at one electrode and OO will form at the other electrode, reversing
the favorable reaction above so it becomes the normally
unfavorable "HOH + HOH --> HH + OO + HH". Or, supplying energy
to a refrigerator can lower the temperature inside it, even though this would
never occur (and it would violate the Second Law) under ordinary circumstances.
But as long as energy continues to flow through the refrigerator, and its "mechanism
that produces cold" is operating properly, the high-entropy cold area can
be maintained, in a way that is consistent with the Second Law. Similarly,
energy flow through our bodies can — due to the mechanisms that maintain
life, that convert food energy into biologically useful functions — maintain
our bodies in a high-entropy state.
The book's authors (Charles Thaxton and Walter
Bradley, plus geologist Roger Olsen) explain why a "coupling
mechanism" is necessary: "Maintenance
of the complex, high-energy condition associated with life is not possible apart
from a continuous source of energy. A source of energy alone is not sufficient,
however, to explain the origin or maintenance of living systems. The additional
crucial factor is a means of converting this energy into the necessary useful
work to build and maintain complex living systems from the simple biomonomers
that constitute their molecular building blocks. An automobile with an
internal combustion engine, transmission, and drive chain provides the necessary
mechanism for converting the energy in gasoline into comfortable transportation.
Without such an "energy converter," however, obtaining transportation
from gasoline would be impossible. In a similar way, food would do little
for a man whose stomach, intestines, liver, or pancreas were removed.
Without these, he would surely die even though he continued to eat. Apart
from a mechanism to couple the available energy to the necessary work, high-energy
biomass is insufficient to sustain a living system far from equilibrium.
In the case of living systems such a coupling mechanism
channels the energy along specific chemical pathways to accomplish a very specific
type of work. We therefore conclude that, given the availability of energy
and an appropriate coupling mechanism, the maintenance of a living system far
from equilibrium presents no thermodynamic problems."
The authors also
emphasize the important difference between producing
a coupling mechanism (during chemical evolution
to produce the first generation of life) and maintaining
it (during many succeeding generations of life, to allow a process of biological
evolution): "While the maintenance of living
systems is easily rationalized in terms of thermodynamics, the origin
of such living systems is quite another matter."
During biological evolution after life is
established and stable, the basic life-allowing mechanisms already exist,
are inherited with sufficient reliability through many generations, and in principle
these basic mechanisms can increase in variety and complexity through a neo-Darwinian
ratchet process so the relevant questions are "What
types of complexity can be produced, and how quickly?" But
in chemical evolution, the basic mechanisms do not exist (so life
cannot exist) but they must be produced (so life can exist), and this
seems much more challenging.
Creationist
Confusions (When is a mechanism needed?)
Young-earth creationists claim that a "mechanism"
is necessary to convert raw energy into useful functions. But sometimes
they don't seem to understand the function of a mechanism, as when the Evolution
Refuter says "the living organism is able to
use free energy from its environment to pay for the creation of the new information."
This is wrong, because "energy from its environment"
doesn't produce the new information. Instead this energy, when it's converted
into useful functions by the mechanisms that already exist inside an organism,
lets the organism live and reproduce, and this can let the natural actions proposed
in neo-Darwinian evolution — gene duplication, mutation, selection,...
— produce new information.
Usually, creationist claims lack clarity,
so we don't know what kind of evolution is being criticized: Is it astronomical
evolution (where a mechanism is not needed because simple attractive forces
are sufficient for the "ordering"), or biological evolution
(when the mechanisms already exist, as described above), chemical evolution
(the only type of evolution where a mechanism does not exist yet is needed and
must be produced), or just evolution in general?
For example, in Entropy
and Open Systems (1976), Henry Morris implies that the "evolution"
is chemical and biological: "The most devastating
and conclusive argument against evolution is the entropy principle. ... The
evolutionary model of origins and development requires some universal principle
which increases order, causing random particles eventually to organize themselves
into complex chemicals, non-living systems to become living cells, and populations
of worms to evolve into human societies. However the only naturalistic
scientific principle which is known to effect real changes in order is the Second
Law, which describes a situation of universally deteriorating order."
Later in his paper, the evolution
is astronomical and biological: "What is the information
code that tells primeval random particles how to organize themselves into stars
and planets, and what is the conversion mechanism that transforms amoebas into
men?"
He also places a "converter
mechanism" at the central core of thermodynamics: "The
Second Law of Thermodynamics could well be stated as follows: In any ordered
system, open or closed, there exists a tendency for that system to decay to
a state of disorder, which tendency can only be suspended or reversed by an
external source of ordering energy directed by an informational program and
transformed through an ingestion-storage-converter mechanism into the specific
work required to build up the complex structure of that system."
Those who understand thermodynamics will not agree with this formulation, because
it ignores the important distinction between open and closed systems (and between
system-entropy and universe-entropy), and the Second Law says nothing about
programs and mechanisms. As explained by Thaxton & Bradley above,
a "mechanism" operates only in specific situations like the biochemistry
of life. As shown in my examples for why things happen,
a decrease in apparent disorder can occur in a wide variety of situations —
such as when particles organize themselves into stars and planets — due
to the simple operation of attractive forces, with no "mechanism"
needed.
Morris even uses the Second Law in his arguments
for a design of nature, when he includes "the electrochemical
properties of the molecules in the crystal" in the many things that
"could never have been produced within the constraints
imposed by the Second Law." Here is the context of his claim,
which mixes questions about standard evolution(s) with a design of nature: "The
highly specialized conditions that enable crystals to form and plants and animals
to grow have nothing whatever to do with evolution. These special conditions
themselves (that is, the marvelous process of photosynthesis, the complex information
programs in the living cell, even the electrochemical properties of the molecules
in the crystal, etc.) could never arise by chance — their own complexity
could never have been produced within the constraints imposed by the Second
Law. But without these, the crystal would not form, and the seed would
never grow."
Proponents of theistic evolution claim
that God designed the universe so its natural characteristics — such as
"electrochemical properties" —
would be sufficient for its development by a process of natural evolutionary
creation. Despite their claim that the universe was designed with a "program"
to allow its development by natural process, Morris insists that they must "demonstrate
that the vast imagined evolutionary continuum in space and time has both a program
to guide it and an energy converter to empower it. Otherwise, the Second
Law precludes it." His own explanatory theory is that,
a few thousand years ago, "The
Creator, both omniscient and omnipotent, made all things perfect in the beginning.
No process of evolutionary change could improve them, but deteriorative changes
could disorder them."
Nine years later — in a paper
asking Does
entropy contradict evolution? (1985) — Morris is still using the Second
Law to argue that molecular machinery is needed for both chemical and biological
evolution: "If the energy of the sun somehow is going
to transform the non-living molecules of the primeval soup into intricately
complex, highly organized, replicating living cells, and then to transmute populations
of simple organisms like worms into complex, thinking human beings, then that
energy has to be stored and converted into an intricate array of sophisticated
machinery."
Does life violate
the Second Law?
No. Although "inside
our bodies, reactions occur that would not occur outside our bodies,"
these life-reactions don't violate the Second Law. This is illustrated
in an example showing that, as always, universe-entropy increases even though
untrained intuitions about "entropy as disorder" might lead to the
opposite conclusion:
Imagine a one-celled zygote (the earliest
form of a baby animal) locked in a room that is closed (with no matter or energy
moving in or out), that is like a miniature universe. There is plenty
of food, water, and air in the room, which is a suitable incubator for the baby
animal to survive and thrive. After a few weeks of growth, the animal
will be much larger and more complex, since it began with one cell and ends
up with more than a trillion cells. But when we
consider all changes in the miniature universe — the initial chemicals
(complex molecules in the food + OO) changing to final chemicals (complex molecules
in the animal + COO + HOH) and the increase in temperature of everything in
the mini-universe due to heat given off by the animal while metabolizing the
food — the entropy will increase, mainly
due to the temperature increase. But if we look only at the animal, the
apparent order seems to have increased (and if we use "tidy --> messy"
logic, the entropy appears to have decreased) as judged by this non-thermodynamic
intuition, which is wrong.
What about the animal? Entropy increases
with size — for example, 5 grams of a chemical will have 5 times the entropy
of 1 gram — and the animal has become much larger, so obviously its entropy
(which is a localized system-entropy) has increased. { But the animal's
entropy-per-gram hasn't changed much; my educated guess is that this has
actually decreased, based on my hunch that a lower percentage of the grown animal
is highly constrained DNA, but I could be wrong. } #true?
In this example, a minor factor in the overall
entropy increase is the complex chemicals (large biomolecules in the food) being
broken down into simple chemicals (a larger number of small molecules, mainly
COO + HOH) that have decreased motional constraints. But we can ask, "How
did the complex food-chemicals become complex? Didn't this previous increase
in size and complexity (and entropy) violate the Second Law?" No.
Sunlight-energy coming into an open system (the earth) was harnessed (by the
photosynthetic mechanisms operating inside plants) and was converted into complex
food molecules with low entropy and high chemical potential energy.
note: Young-earth creationists don't
claim that any of this violates the Second Law, since the systems meet the creationists'
own special requirements: open systems with an "informational
program" that produces a "converter mechanism."
The Second Law
in Life and Death
Is there a correlation between the
Second Law and bodily deterioration? No. The Second Law is
operating, not just when our bodies deteriorate and die, but also when our bodies
grow larger during youth and adolescence, when we stronger in response to exercise,
when we feel refreshed after awaking from sleep, and when we recover from illness.
Consider a quickly growing infant, a healthy person in the prime of life, a
sick person getting weaker every day, an old person whose body is slowly deteriorating,
a victim of disease who is nearing death, a suddenly-lifeless corpse, and a
corpse that has been decaying for a week or a decade. Each
of these is equally governed by the Second Law, which is what makes all reactions
occur, including the chemical reactions that allow life, health, and growth.
In the biochemistry of our bodies, the difference
between life and death is equilibrium, not the
Second Law. While we're living, the biochemical reactions within our bodies
are trying to reach equilibrium but (on the whole) are failing. While
we're living, biochemical energy — obtained from the food we eat and the
air we breathe — keeps our bodies "away from equilibrium" but
when we die the chemical reactions can finally begin to reach equilibrium, first
in the life-giving reactions of metabolism and continuing through a long process
of decay. During the whole process, from conception to death and afterward,
the Second Law is operating in the same way, so the chemicals can "do what
comes naturally" in their reactions.
Should we still ask questions? •
When critics hear claims that the Second
Law is a "devastating and conclusive argument against
evolution," they correctly explain that the process of life, continuing
through many generations, is allowed by the Second Law due to the flow of energy
from the sun into plants, which then provide energy for animals. Also,
the two major actions of evolution — mutation and natural selection —
are consistent with the Second Law, and so is a long step-by-step evolutionary
process involving these two actions. But just because biological evolution
is possible because solar energy allows life to continue through many
generations, this doesn't indicate that natural evolution was sufficient
to produce everything that occurred in the historical development of life.
We can still ask important scientific questions about rates of change, irreducible
complexity, and more, as discussed earlier.
Also, appeals to an inflow of solar energy
don't address the important difference between chemical evolution and biological
evolution, between producing a coupling mechanism
(in the first generation of life) and maintaining
it (through succeeding generations). This difference is acknowledged by
Thaxton & Bradley: "While the maintenance of
living systems is easily rationalized in terms of thermodynamics, the origin
of such living systems is quite another matter." Some of their
questions about the origin of life are below.
APPENDIX
Thermodynamics
and The Origin of Life
Scientists have proposed a two-stage
process for a natural origin of life: reactions form organic molecules
which combine to make larger biomolecules (like proteins and RNA), which
then self-organize into a living organism. For the first stage,
a major problem is that many essential reactions are "uphill"
in energy. Walter Bradley illustrates downhill-reactions and uphill-reactions
by analogy with a pool table. Here is my paraphrased summary:
Imagine a hemispherical valley in
the middle of a horizontal billiard table that has no pockets.
We place 10 pool balls on the table, then gently agitate the table.
Eventually, all balls end up in the valley. Without the valley
this clustering would have a low probability (and low entropy), but
with the valley it has the highest probability (and highest entropy).
There is less "apparent disorder" but entropy (of the universe)
has increased, consistent with the Second Law.
Bradley explains that "the
difficulty in getting polymerization condensation reactions is that
our pool table [doesn't have a valley]... it has a hill. ... One
might conclude that the formation of protein and DNA via polymerization
condensation reactions is well nigh impossible. ... The only solution
to this dilemma is to do some very specific work on the system to assist
these balls up the hill. ... This work must be very carefully
done so as to not jar loose the balls that are already there.
Thus, the energy must be selective in getting the balls up the hill
while at the same time not causing the balls there to be removed from
their positions of metastable equilibrium."
Many reactions occur because, as
illustrated in Sections 3A and 3B, a small unfavorable change in entropy
is overcome by a large favorable change in energy. But with many
reactions that are essential for life, the changes in entropy and energy
are both unfavorable. A living organism can make these unfavorable
reactions occur by coupling uphill-reactions with downhill-reactions,
to make the combination energetically favorable. But in an "origin
of life" scenario the coupling mechanisms would not be available.
Thaxton & Bradley say, "While the maintenance
of living systems is easily rationalized in terms of thermodynamics,
the origin of such living systems is quite another matter."
The question of an energy-harnessing mechanism — which was not
needed for astronomical evolution, was available for biological evolution,
but was needed yet not available for chemical evolution — is discussed
earlier. {more about the
origin of life}
Information and Entropy
One problem for a natural origin
of life is that even if biomolecules did form, despite the unfavorable
reactions described above, an extremely small fraction of these biomolecules
would be useful. Thaxton & Bradley claim that this low probability
is a low "configurational entropy" and they explain the difference
between two types of entropy:
"Consider
the case of the formation of protein or DNA from biomonomers in a chemical
soup. For computational purposes it may be thought of as requiring
two steps: (1) polymerization to form a chain molecule with an
aperiodic but near-random sequence, and (2) rearrangement to an
aperiodic, specified information-bearing sequence. The entropy
change associated with the first step is essentially all thermal
entropy change, as discussed above. The entropy change
of the second step is essentially all configurational
entropy change."
Their claim seems credible, since
the number of microstates associated with
all possible biomolecule-sequences (after Step 1) is much larger than
the microstates associated with a specific biomolecule-sequence (after
Step 2), so there has been a large decrease in probability (and thus
entropy) during Step 2, and this is the "configurational
entropy change." We can also think
about this entropy change as the "information" that is needed
to specify the specific sequence.
Entropy and information are distantly related because both are related to complexity, but they are basically different. Credible
questions about the development of biological information have been
asked, first by Thaxton & Bradley (described in terms of thermodynamics) and
later (mainly using information theory) by William Dembski, Steve Meyer,
and other design theorists. Their questions about chemical evolution
and biological evolution are worthy of serious consideration, and scientists
are currently debating the merits of their claims.
Currently, I'm included among the
scientists who are debating the merits. I'm not
sure what I think about this, for two reasons: the questions
are scientifically challenging, with good arguments on both sides,
and I think that we
(as a scientific community) don't know enough to confidently decide
one way or the other; more important, I (as a person) certainly don't know
enough, so I'm in the process of learning more about the claims
and
counter-claims, and the relationships between information theory and
thermodynamics. Eventually (probably by the end of April 2010)
I'll write
a little more about this, and will provide links to educationally useful
pages.
A
Range of Quality (in Creationist Thermodynamics)
comment:
Either in this appendix or (more likely) in another page, I'll review
web-pages (about entropy, Second Law,...) by young-earth creationists.
All of the pages I've seen have some good ideas mixed with some scientific
errors and unwarranted claims, but the quality varies; some pages
are fairly good overall, while others make too many erroneous claims.
And in an effort to help clean up
the "four-alarm mess" so we can more accurately understand
their views, I'll find responses from creationists who will clarify,
and I'll provide links to these pages here and in the resource-pages
for the science
and theology of
thermodynamics.
Does the
Second Law describe what WILL happen?
The Second Law claims that "whatever
is most probable is most likely to happen" but not
"whatever is most probable will happen," for two reasons:
A) Claims made by the Second Law are always probabilistic, even for
systems (including most chemical systems) containing such a huge number
of particles that probability is almost certainty, and the occurrence
of anything except "what is most probable" is extremely improbable,
almost impossible. B) But with some reactions — including
biologically important reactions such as genetic mutations — there
is significant uncertainty about what will happen in the equilibrium
state. [IOU - why probabilistic? is this the reason?]
Free Energy Changes: Standard and Actual
In Section 3B
the values of DH, DS,
and DG are for chemicals at standard
conditions for temperature (25 Celsius) and concentrations (1
mole/liter, 1 atmosphere,...). These values (for DH,
DS, and DG) change
when chemicals are not at standard conditions, but the standard values
are usually a good approximation to the actual values, which can be
calculated using the actual conditions.
Irreversible
and Reversible
Below its melting point (for example, at -1 Celsius)
liquid HOH will undergo an irreversible reaction
to form solid HOH, which at this temperature is more thermodynamically
stable. Above its melting point, at +1 C, the situation is reversed
and solid HOH will undergo an irreversible reaction to form liquid HOH,
which at this temperature is more stable. At the melting point,
at 0 C, both phases are equally stable, so they can remain in a "part
solid and part liquid" mixture; but if heat is added extremely
slowly, solid can be converted into liquid (but with the T remaining
at 0 C) in a reversible reaction;
and liquid can be converted to solid (remaining at 0 C) in a reversible
reaction if heat is removed extremely slowly.
The Second Law states that universe-entropy
will increase in an irreversible reaction, and will remain constant
in a reversible reaction.
But a reversible reaction is an idealization,
a useful fantasy, like a "frictionless surface" in the thinking
of Galileo or Newton. In reality, all reactions
are irreversible because the conditions necessary for a reversible
reaction — such as no friction, or infinite time (needed for melting
ice at an infinitely slow rate if its temperature is infinitesimally
above the melting point) — don't occur in reality.
During dynamic
equilibrium, counter-balancing "reactions that are reversible"
occur at the microscopic level of molecules, even though (by the definition
of equilibrium) no change is occurring at the macroscopic level.
For example, at 25 C a cup of liquid-HOH is in equilibrium (at 100%
humidity) with gas-HOH at a pressure of .0313 atmosphere, but during
each second zillions of liquid-HOH molecules are evaporating from the
cup to form gas-HOH, which is balanced by the zillions of HOH-gas molecules
that are condensing into liquid-HOH, so no net change is occurring.
The situation is dynamic (because zillions of reactions are happening)
and is at equilibrium (because there is no net change). But a
reversible reaction requires change, so dynamic
equilibrium is not a reversible reaction.
Sometimes entropy is important at low temperatures.
comment
-- I'll try to find examples of these, probably from biochemistry.
Three Sets
of Terms (for Three Types of Systems)
In thermodynamics, there are three
types of systems, which differ in "what is transferred" across
the system's boundaries: • nothing (not mass and not energy),
• energy but not mass, •
both energy and mass.
There are two sets of terms for these systems, as you can see below
in #1 and #2. This can cause confusion, because "closed"
has two meanings (which differ in #1 and #2, and seems wrong in #1),
and "open" has two meanings in #2.
| What can transfer? |
#1-terms |
#2-terms |
my terms |
| • not energy, not mass |
isolated |
closed |
isolated |
| • energy
but not mass |
closed |
open |
semi-open |
| • both energy
and mass |
open |
open |
open |
In this page, I'm using two terms from #1 because it seems to be the
conventional terminology, but I'm refusing to use "closed"
because it seems wrong to call a system closed
when it is open to a transfer of
energy, which is the most important thing in thermodynamics.
|
This website for Whole-Person Education has TWO KINDS OF LINKS:
an ITALICIZED LINK keeps you inside a page, moving you to
another part of it, and
a NON-ITALICIZED LINK opens another page. Both keep everything inside this window,
so your browser's BACK-button will always take you back to where you were.
|
Here are other related pages:
This page is
http://www.asa3.org/ASA/education/origins/thermo2.htm
Copyright © 1998 by Craig Rusbult
all rights reserved