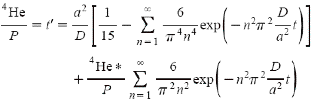
Helium Diffusion
and Retention in Zircons
by Randy Isaac, Ph.D.
This page supplements an introductory paragraph in the author's essay
review and a brief technical overview in a general
reply that is part of
a scientific examination of RATE.
The
objective of the RATE project was to examine issues of radioactivity
in regards to the age of the earth.1 A short review of the
RATE project has been published elsewhere2 as well as the
RATE team’s response.3 This article seeks to elaborate
in more detail the specific example of the RATE team’s analysis of
dating zircons with helium.
The
chapter on dating zircons with helium was authored by D. Russell Humphreys
who has published numerous articles in creationist journals on this
topic. His chapter presents a “new creation model” and a “uniformitarian”
model. This article will assess the validity of three models: the standard
model which is typically used by geochronologists but
was not discussed by the RATE team, the RATE team’s “new
creation model,” and the model the RATE team calls the “uniformitarian
model.”
The Standard Model
The criteria for a valid dating
technique include a physical model in which time is the only unknown
and all other parameters can be measured experimentally. It also requires
a physical event that triggers the clock for a meaningful measurement
of age. Zircons are typically dated with radiometric techniques based
on U and Th decay. The helium content of zircons is not used to date
the formation of the zircon but rather to garner clues to the thermal
history. At high temperatures, helium readily diffuses out of the zircon. Any helium generated by alpha-emitting radioactive elements easily escapes
from the mineral. At low temperatures, helium remains trapped in the
zircon and the concentration increases as the alpha emitters generate
more helium. The transition temperature is called the closure temperature
and is typically on the order of 200oC but is dependent on
the geometry as well as the diffusivity.
The helium clock in a zircon
starts when a zircon cools to the closure temperature. It may have had
a varied thermal history prior to that but the high diffusivity above
the closure temperature erases any record of it. Below the closure temperature,
the helium concentration grows from the continuous generation of alpha
particles from radioactive members of the U-Th decay series. The concentration
and decay rate of these alpha-emitters can be measured as well as the
current concentration of helium. Using the simple equation Q = Pt
where Q is the current helium concentration, P is the
alpha generation rate and t is the time since the mineral cooled
below the closure temperature, the time t is the only unknown and both
Q and P can be measured. The ratio Q/P has units of
time and is known as the helium age of the zircon.
A more sophisticated mathematical
treatment that fully accounts for both helium outdiffusion and helium
generation as well as initial helium concentrations, is given by Wolf,
et.al.,4 for the simplified case of spherical symmetry:
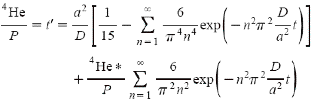
where 4He
is Q , the current concentration of helium, and 4He*
is Qo , the original concentration of helium
at t=0 , P is the rate of helium generation, a is the radius
of the sphere, and D is the diffusivity. From this equation
we can see that the time constant of the physical system is a2/Dp2. For
time periods of about 5 time constants or more, the system will
be in steady state with a helium age of a2/15D. The
diffusivity is exponentially dependent on temperature and as the mineral
cools, it will take a very long time for the crystal to achieve
steady state.
The second term of the equation
decreases over time so that the influence of any initial helium concentration
will be negligible after about 5 time constants. This quantifies the
assumption made earlier that at high temperatures, any original helium
will have escaped the crystal. The first term of the equation will always
increase with time until the steady state condition is reached. This
is physically consistent with a system where the sole source of helium
is alpha production from radioactive decay and where outdiffusion is
negligible. The helium concentration will decrease in time only if equilibrium
is affected in such a way that the concentration exceeds the steady
state value. This can happen if the temperature increases, causing the
diffusivity to rise significantly and lowering the steady state value. Another
mechanism for altering the steady state value would be if the generation rate
P were to rapidly decrease significantly. If, for example, the alpha-emitters
were quickly depleted or leached out of the system, the generation rate would
drop and the helium concentration would be larger than its new steady state
value and would subsequently decrease gradually. Though zircons may
have had a history of fluctuating temperatures, geological records indicate
that
the recent past has been a slow cooling mode.
This equation also serves to
bound the case in which the simplified model of Q=Pt can hold. For
systems with negligible initial concentration of helium, and for time
short compared to the time constant, the equation reduces to a
good approximation, Q=Pt.
Wolf, et.al., apply their
model to apatite crystals and find values of helium ages on the order
of 50 million years, in good correlation with other techniques. Their
work explores the usefulness of helium thermochronology and is also
applicable to zircons.
The New Creation Model
In the RATE project, Humphreys
takes a different approach. Instead of the standard technique of using
the helium retained by zircons, he uses a diffusion dating method based
on the helium that is lost. He assumes that at t=0 the zircon
had a helium concentration of Qo which decreases
over time to its current value of Q through outdiffusion, and
assumes that helium generation from alpha-emitting radioactivity is
negligible.
This model fails to meet the
basic criteria for a good dating technique. It is far more difficult
to measure the helium that is missing than the helium that is present. There
is no direct measurement of Qo nor is
there a physical mechanism that would start the clock for a determination
of time. This method also relies very sensitively on knowledge of
the diffusivity and thermal history of the mineral. Any calculation
from this model would not be relevant for any physical parameter.
Undeterred, Humphreys proceeds
to estimate all the unknowns. To determine Q , he sent his own
samples to a reputable experimenter to measure both helium content and
diffusivity. Most of his results, however, are based on samples obtained
by Gentry.5 Humphreys takes Gentry’s published measurements
of Q and adjusts them by a factor of 10 with no other explanation
than it was done after private communication with Gentry. With no knowledge
of the reason for the adjustment, it is impossible to comment on its
validity.
To determine Qo ,
Humphreys relies on Gentry’s calculation of the retention factor,
Q/Qo . Those values are given in the following
table by Gentry:
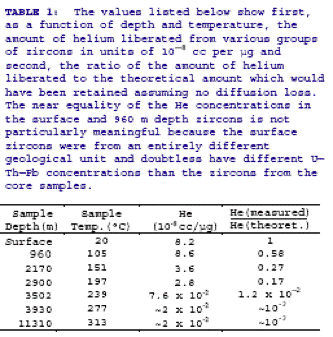
Humphreys
interpolates those
numbers for his own samples. No clear explanation is given for the way
in which Gentry obtained these retention factors nor their meaning. The only
comment in this regard is Gentry’s
note that:
“Knowledge of the zircon
mass and the appropriate compensation factor (to account for differences in initial
He loss via near-surface
a-emission) enabled us to calculate the
theoretical amount of He which could have accumulated assuming negligible diffusion
loss. This compensating
factor is necessary because the larger (150-250 mm)
zircons lost a smaller proportion of the total He generated within the crystal
via near-surface a-emission than did the
smaller (40-50 mm)
zircons. For the smaller zircons we estimate as many as 30-40% of
the a-particles (He) emitted within the
crystal could have escaped initially whereas for the larger zircons we studied
only 5-10% of
the total He would have been lost via this mechanism. The ratio of the
measured to the theoretical amount of He is
shown in the last column of Table 1. The uncertainties in our estimates
of the zircon masses and compensation factors probably mean these last
values are good only to ±30%.”
It is not at all clear that
Gentry’s theoretical concentration of helium can correctly be interpreted
as an initial concentration Qo of helium. If
so, how did Gentry make that calculation? What were his assumptions? If
Gentry’s calculation is based on an estimate of all possible helium generated
by alpha-emitters in the 1.5 billion year age of the zircon, corrected for near-surface
losses, then the RATE team’s assumption that at some time in the past the
zircon contained a helium concentration of Qo cannot
be supported. That amount of helium was never concentrated in
the zircon at the same time.
The physical mechanism that
Humphreys proposes to explain an initial value of Qo with
a subsequent decrease in concentration is that accelerated nuclear decay during
Noah’s flood caused a very large alpha generation rate
which then dropped to its current value. Subsequent discussion by the
RATE team shows that the justification for speculating that accelerated
nuclear decay occurred is based largely on a young earth as determined
by helium diffusion in zircons. This is circular reasoning at best. Nuclear
decay rates have long been shown to be constant and there is no independent evidence
to support any deviation.
Humphreys uses diffusion data
from the experimenter to which he sent his own samples and also the
diffusivity data that Gentry provided. As is typical, these data are
taken at higher temperatures and extrapolated down to the regime close
to the closure temperatures and ambient temperatures at which the samples
were found. He makes the approximation that the diffusivity is constant
over time to simplify the calculation. In this temperature range, the
diffusivity is highly uncertain and strongly dependent on the physical environment
and structure.6
At this point, Humphreys takes
two directions. First, he assumes that t=6,000 years and calculates
the diffusivity that would be required to lose the amount of helium
indicated by Gentry’s retention factor. Amazingly, the answer is close
to the measured diffusivities. Then, he assumes the measured diffusivity
and calculates the time required to lose that helium. The answer is
on the order of 6,000 years. On this basis, the RATE team concludes
that helium diffusion provides evidence for a young earth.
The model proposed by the RATE
team fails to meet the basic criteria for a dating technique and any
values calculated from the model have no relationship to any physical
parameter. The team speculates on the physical system and possible values
of the physical constants and then performs a complex numerical solution that
doesn’t
converge
easily,
according to their report.
The
Uniformitarian Model
The RATE team then turns to
assessing what they call the uniformitarian model. The name is intended
to imply an assessment of how geologists normally date zircons. But
the model has no relationship to the standard model. Instead, Humphreys
notes without calculation that with so much time, the crystals would
surely be in steady state. He then derives the steady state equation
to be Q/Qo=a2/15Dt. He
notes that Qo/t is the alpha generation
rate which is essentially constant but then he fails to note that the
parameter t cancels out of the equation as it should for a steady state
condition. In that case, the equation is identical to that discussed
in the standard model. However, Humphreys chooses to identify Q/Qo as
Gentry’s retention factor and arbitrarily inserts 1.5 billion years
for the value of t on the right hand side. He then calculates a value
of D that is five orders of magnitude lower than his measured
values and derisively concludes that the uniformitarian model is hopelessly
flawed. It is indeed true that the model he presents is hopelessly flawed. There
is no reason to believe that the steady-state condition has
any relationship to Gentry’s retention factor nor is there justification
for using 1.5 billion years. {comment, added 2-24-08: In
essence, the RATE team’s
version of the solid-state condition equates Gentry’s retention factor
to the ratio of the helium age to the age of the zircon as determined from
standard dating techniques based on U, Th, and Pb. Though there is not sufficient
information about how Gentry derived his retention factors, the typical values
of helium ages in zircons are in the tens of millions of years, in good harmony
with the typical ages of zircons of 1.5 billion years. There is no fundamental
discrepancy.} More importantly, a steady state
equation should not have time as a parameter. There would be no change over
time in a steady state mode. This model has no relationship to any model
used in thermochronology.
Conclusions
In summary, when we consider
three models for using helium to date minerals, we find that only the
standard model meets the criteria for a useful dating technique. The
RATE team uses models that do not relate to what is known physically
about zircon formation. No amount of fine-tuning of the parameters would
correct the fatal flaws of the models. Neither the new creation model
nor the so-called uniformitarian model provide any insight to the history
of a real zircon.
We conclude therefore that
helium dating of zircons leads convincingly to dates that are consistent
with standard zircon dating methods. Helium ages on the order of tens
of millions of years are consistent with measured zircon ages of a billion
or more years. Helium diffusion in zircons provides evidence that the
earth cannot be thousands but must be billions of years old.
REFERENCES
1) L Vardiman, et.al., Radioisotopes and the Age of the Earth, Vol.
2, Institute
for Creation Research, 2005.
2) R Isaac, Perspectives on Science and Christian Faith, Vol. 59,
No. 2,
p. 143. {full text}
3) L Vardiman, et.al., Perspectives on Science and Christian Faith, Vol.
60, No.
1, pp. 35-36. {full text}
4) RA Wolf, KA Farley, and DM Kass, Modeling of the temperature sensitivity
of
the
apatite (U-Th)/He thermochronometer: Chemical Geology, Vol. 148, pp 105–114
(1998). {abstract}
5) RV Gentry, Geophysical Research Letters, Vol. 9, No. 10, pp 1129-1130,
Oct 1982. {full text}
6) R Whitefield, The RATE Project Claims [about accelerated decay, and
helium
in
zircons] {full text}
More about RATE (by Randy Isaac and others)