Time, Chaos Theory and the Thought of 
Michael Polanyi

J.W. STINES

Department of Philosophy and Religion
Appalachian State University
 Boone, NC 20608

From: Perspectives on Science and Christian Faith 44 (December 1992): 220-227.

Chaos theory is only recently breaking into the consciousness of the philosophical and scientific communities on a large scale; hence, exploration of its philosophical and theological implications has barely begun. This paper undertakes to sketch some key aspects of chaos theory, especially in relation to the notion of temporality, and to suggest that the import of chaos theory for our way of thinking about time calls for a dialogical biblical way of modeling it -- such as is richly implicit in the works of Michael Polanyi -- rather than the classical tragic way which has dominated traditional science.

Change and Continuity

If a speaker should suddenly interrupt his or her address and run amok among the audience, crawling on all fours, barking and biting at people's heels, he would create a great deal of angst - perhaps a feeling in the pit of the stomach that there is an abyss underfoot of which such apparent insanity is only a token. We tend to be made alternatively curious and anxious by anomalous phenomena and tend to believe, even if such strange behavior did occur, that it is not really anomalous, but an outcome of certain conditions which, had we been privy to them, would have made it predictable. That is, there is an almost overwhelming classical rationalist and classical tragic tendency in us. A part of us cannot imagine any particular moment in time as having meaning or as being psychologically bearable except insofar as it is finally viewed as subordinated to, and a manifestation of, structure and continuity. The alternative seems to be irrationality - cognate to chaos, cognate to meaninglessness.

When, in Sophocles' Oedipus Rex, the power and the very ground of predictability seem, momentarily, to have been falsified by the out-standingness of Oedipus - his apparent escape from his place of destiny and the predictions of the Delphic oracle -- Jocasta says, half in relief and half in despair: "How can a man have scruples when it's only chance that's king? There's nothing certain, nothing preordained; it's best to live by chance as best we may."¹ But, of course, this sense of Oedipus' exceptionality is only momentary; and in the end there is relief in the realization that there is no suspension of the order which makes prediction possible and justice itself a reality. Spring will follow winter. Time, after all, to paraphrase Plato, is simply the moving re-presentation of the universal, the eternal and unchanging.

However, there is another dimension to our humanity which is more deeply resonant with Oedipus in his moment of exceptionality and which chafes under the subordination of the apparently novel and particular to the universal. It is that side of us which is manifest in the sense of the personal; it protests on behalf of the reality and the uniqueness of every person as such and is outraged by their subordination to the abstractions of timeless structure. All of us know that it is a personal insult to have someone look out of the corners of their eyes and say, "Humph! I know you." We are inclined to respond by showing just how unpredictable or unknowable we really can be. However, we don't really know what to do with this sensibility, since "true" scientia seems to render it illusory. The reality of the individual moment in time seems, as such, to be as intolerable and paradoxical as the phrase "chaos science." Correlatively, we have forgotten or denigrated the underpinnings of this sensibility in the Judeo-Christian tributary to our imaginations. In the Enlightenment tradition we asked whether Athens and Jerusalem have anything to do with each other. Both explicitly and implicitly we answered, at least intellectually and academically, in the negative, by coming down on the side of Athens, the side of the predominance of structure and necessity and, correlatively, on the side of objectivity and the dominance of the visual metaphor for describing our situation in knowing and being.

The Greek word theoreo meant "to look at," "to view," "to build," and "to know." That is, knowing in the classical rationalist context was affiliated with seeing in the sense of spectating. Reality is observed; it is given independently of the participation of the observer, the theoretician. To use a phrase of W.H. Poteat's, it is imagable as a series of closed "slices of dead space."² The real is pure form; and to no spectator or re-presenter of it would it occur to include, if you will, wild hairs, bulbous flesh, individual electrons, turbulence, implications of decay, a-rhythmia, passion or, in the language of chaos theory, "strange attractors," unless, perhaps, by a Platonic move to show their subjugation to a super order.

In ancient Israel there was a strikingly different mythos or paradigm of the real and the relation between change and continuity. Here was the sensibility that reality is intractable to mere seeing. No visual or purely theoretical relation to it is adequate or finally appropriate. It is not necessity which reigns, but contingency. The present is a real presence which might have been otherwise, since it is not a re-presentation of a timeless, mute, impersonal structure and necessitated by it. Human beings with proper names, in their concrete embodiment in time, stand in a dialogical relationship to and with reality. The dominant metaphor is oral-aural and timeful rather than visual-spatial. Correlatively, there is no history-nature or knower-known dichotomy, but an indissoluble dialectical relatedness. (It turns out that even God responds to human response.)

Now I take it that this sensibility is a bit like that dialectical situation which, to those physicists who are inveterate Athenians, is one of the implicit horrors of the Copenhagen interpretation of quantum indeterminacy. The what question cannot be separated from the how question. Knowledge as mere seeing or detached spectation is systematically elusive. The knowing subject in his or her historical contingency is a participant. He has to address nature in some particular way or "speak" to her, if you will, in order to get her to disclose herself. And how she answers is not independent of how she is addressed.

For biblical thought, both monotony and novelty, both continuity and change are seen as aspects of God's sovereign (hence uncoerced or unnecessitated) will in relation to his creation.³ Predictability and order are but the outward manifestations, not of an a priori necessity, but of God's faithfulness; "yet he is choosing to be faithful anew, in every moment, with the result that there is real novelty both in the orderly and outside it."⁴

The apparently novel may be really novel in the way every one of an individual's acts-as action in distinction from mere reaction - is novel. "But at the same time it need not be meaningless because irrational, i.e., form-defying."⁵ For however erratic may seem the act of a person whom you deeply trust, "however defiant of your power to put it into a finite and hence comprehensible context of interpretation, it may nevertheless be meaningful to the infinite context open to faith" and full participation in the personal dialogue.⁶

Recall Job's miserable and utterly baffling condition - so baffling that Job's wife, in full rebellion, says "Curse God, and die." Job, in effect, answers her that, "Though he slay me, yet will I serve him." The novel, unpredicted act of will cannot always be known to be rationally related to the stable purposes of that willing person. But it need not for that reason have no relation whatever when we grasp the act as proceeding from the will of a person we trust profoundly.⁷

Hopefully, personal quarrels with theism will not obscure the force of the analogies at issue here. Surely this latter way of modelling change and continuity is not, at its core, any more insane than the Athenian way; and it has the merit of being closer to our concrete personal experience, which affirms both the significance of particulars and of time as such and of continuity.

Chaos Theory: Non-Linearity

Now what, if anything, has all of this to do with chaos theory? If what I take to be a major import of chaos theory is correct, it may force a revolution - perhaps wider in scope than quantum theory - in the fundamental metaphors which govern our thought about rationality and knowledge in relation to change and continuity. Some of the reported phenomena underlying chaos theory were met, initially, with complete incredulity; however, it presently appears that chaos theory will stand alongside relativity and quantum theory as a major moment in twentieth century science. We have opportunity here to point to only a few paradigms and some of their apparent implications.

At the outset we can say that, in light of chaos theory, systems "ain't what they used to be." At the heart of the traditional perspective on systems (Godel's theorem notwithstanding) is the notion of continuity. A clock is a system, indeed a kind of system of all systems, insofar as it provides a picture of regularity itself which is a direct reflection of the determinism or continuity of physical law. Understand the laws of nature, the regularities, and you understand the universe, which is then itself a kind of clock whose movements, in principle, must be fully determined from "behind" and thus predictable. We recall the famous LaPlacean claim that if a supreme intelligence could see completely into the world system for just one slice of time, it could embrace in one formula all of the past and all of the future. In short, nothing can come out of a system so conceived which isn't aboriginally or timelessly, universally and predictably, in it. Several major aspects of chaos theory seem to cut squarely across this vision. The life of the electron apparently contradicts it at the micro level; but chaos phenomena do so at all levels.

In the new sense chaos may be said to be 
"orderly disorder created by simple processes."

Now it is important at the outset to disaffect ourselves of the tendency to equate "chaos," as used in the present context, with mere noise or meaninglessness. Some people in this field of studies are loathe to use the term "chaos" because of this tendency. But there is probably no single definition of the field that is a happy one for all of its explorers. In the new sense chaos may be said to be "orderly disorder created by simple processes."⁸ Part of the import of this is that the simple linear relation implied by "If A, then B" has been subverted by our discovery that in many cases initial determining conditions may have complex and unpredictable consequences so that, though given A, we know not what the consequences except in very broad terms. Roderick Jenson, a theoretical physicist at Yale working on chaos theory in relation to quantum phenomena says that chaos theory is focused on "the irregular, unpredictable behavior of deterministic non-linear dynamical systems."⁹ The so-called "chaos cabal" at the University of California at Santa Cruz was attracted, as Doyne Farmer, a physicist, put it, to the notion that you could have determinism but "not really." Farmer said:

 The idea that all these classical deterministic systems we'd learned about could generate randomness was intriguing...You can't appreciate the kind of revelation that is unless you've been brainwashed by six or seven years of a typical physics curriculum. You're taught that there are classical models where things are determined by initial conditions, and then there are quantum mechanical models where things are determined but you have to contend with a limit on how much initial information you can gather. Nonlinear was a word that you only encountered in the back of the book. A physics student would take a math course and the last chapter would be on nonlinear equations. You would usually skip that, and, if you didn't, all they would do is take these nonlinear equations and reduce them to linear equations, so you just get approximate solutions anyway. . . . We had no concept of the difference that non-linearity makes in a model. The idea that an equation could bounce around in an apparently random way - that was pretty exciting. You would say, "Where is this random motion coming from? I don't see it in the equations." It seemed like something for nothing, or something out of nothing.¹⁰

As chaos phenomena emerged as the focus of attention there was both dismay and enchantment. Why hadn't this been part of what we were taught?

Norman Packard, another member of the Santa Cruz group, said:

It was striking to us that if you take regular physical systems which have been analyzed to death in classical physics, but you take one little step away in parameter space, you end up with something to which all of this huge body of analysis does not apply.

The phenomenon of chaos could have been discovered long, long ago. It wasn't, in part because this huge body of work on the dynamics of regular motion didn't lead in that direction. But if you just look, there it is.¹¹

What this "it" is that is there "if we just look" is almost as richly present as the concrete non-idealized everyday world in which we exist - a world alive with turbulence. The story is told that Werner Heisenberg said that on his deathbed he would have two questions for God: Why relativity and why turbulence? And Heisenberg says, "I think he may have an answer to the first question."¹²

Classical illustrations of some of the phenomena at issue in chaos theory are to be found in Edward Lorenz's waterwheel and in the Mandelbrot set. In the early sixties, Edward Lorenz, a research meteorologist at M.I.T., accidentally discovered what has come to be called "The Butterfly Effect" or what is referred to in more technical jargon as "sensitive dependence on initial conditions" - the realization that incredible richness and unpredictability can emerge from simple initial determining conditions. Lorenz turned aside from weather prediction to look for simpler ways to produce the complex behavior he had discovered there. He discovered a way in three non-linear equations. Those equations correspond perfectly to a simple mechanism which came to be known as the Lorenzian Waterwheel.¹³ (See Figure 1.)

The water enters from the top at a steady state. If the flow is too slow the friction of the wheel is not overcome,

 and it never starts turning. When the speed of flow is increased the wheel is set in motion and can continue in motion at a steady rate with buckets filling (A) and emptying (A') rhythmically. However, if the flow is made still more rapid the spin becomes chaotic. Some of the buckets fail to fill (B) and some fail to empty (B').

As buckets pass under the flowing water, how much they fill depends upon the speed of spin. If the wheel is spinning rapidly, the buckets have little time to fill up. . . . Also if the wheel is spinning rapidly, buckets can start up the other side before they have time to empty. As a result, heavy buckets on the side moving upward can cause the spin to slow down and then reverse.¹⁴

Lorenz found that over time the spin can reverse itself many times without ever settling down to a steady state or repeating itself in any predictable pattern. A kind of inveterate "common sense" about such a simple system would tell us that if the stream of water never varied, a steady state would evolve. "Either the wheel would rotate steadily or it would oscillate steadily back and forth, turning first in one direction and then the other at constant intervals."¹⁵ But it doesn't. The map, correlated to the three equations, with three variables which describe the system, displays endless complexity. It stays within certain bounds but never repeats itself and traces a "kind of double spiral in three dimensions, like a butterfly with its two wings."¹⁶ No point or pattern of points ever recurs - hence, a kind of orderly, pure disorder. The image of the spiral became known as the Lorenz attractor, an instance of the sort of phenomena later designated "strange attractors." Lorenz's paper on the equations was entitled "Deterministic Nonperiodic Flow" and was a definitive moment in the emergence of chaos theory. The waterwheel phenomenon was seen in important aspects to be analogous to properties of rotating cylinders of fluid in the process of convection. A colleague of Lorenz at M.I.T. was a professor of applied mathematics, Willem Malkus. Confronted with Lorenz's claims, Malkus laughed and said, "Ed, we know - we know very well - that fluid convection doesn't do that at all. The complexity would be damped out and the system would settle into a steady regular motion." Years later Malkus built a Lorenzian waterwheel for his own basement laboratory to show non-believers. He said of early responses to Lorenz's findings, "Of course, we completely missed the point. Ed wasn't thinking in terms of our physics at all."¹⁷

Another paradigm is the Mandelbrot set. It is, in effect, a program, a formula for generating chaos - another kind of picture of non-linear determinism. It involves an iterative process in which a number is put into an equation, and the resultant number is plowed back into it in an indefinite series of iterations. Without presuming to go into the equation itself we can note that the result of its iterations, graphically depicted on a computer screen (a work undertaken by mathematician John Hubbard), is full of incredible complexity and surprise. Mandelbrot had fathered the notion of shapes which are expressions of fractional dimensions and called them "fractals." He

Fig. 2.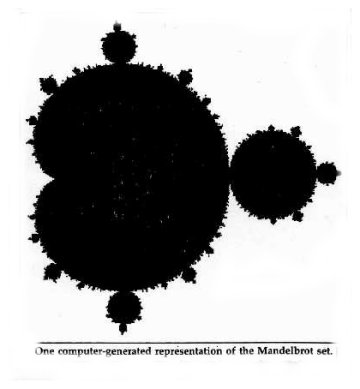

 believed that the recursiveness of fractals reflects something that takes place in the complexity of everything from clouds, to shorelines, to treescapes.

However, when the Mandelbrot set was explored by increasingly powerful computers and examined under increasingly powerful magnification, what emerged were boundaries which were fractal, but not merely recursive. If boundaries between shapes and scale and period spaces were merely fractal recursive, then one iteration of the Mandelbrot set should look more or less like the last. The recursiveness of fractals, the "self-similarity at different scales" would, in theory, make it possible to predict what the electron microscope would see at the next level of magnification. However, each exploration deeper into the Mandelbrot set brought new surprises. "The set did prove to contain, when magnified enough, rough copies of itself, tiny buglike objects floating off from the main body; but greater magnification showed that none of these molecules exactly matched any other. There were always new kinds of sea horses, new curling hot house species. In fact, no part of the set exactly resembles any other part, of any magnification."¹⁸ New molecules were surrounded by their own configuration and so on and on - new worlds, always similar, but never identical, seemingly marching to some sort of "mandate for infinite variety," predictable yet unpredictable.

A corollary of these and cognate developments - especially important as scientists moved from the Mandelbrot set itself to the problems of its relation to non-artificed physical phenomena - had been the emergence of the idea of the "strange attractor." Unlike the attractors of two dimensional phase space in which complete knowledge of a dynamical system can be extracted from a single instant in time, rendering the system representable as a single point, the so-called strange attractor (the insight of physicist, David Reuelle, and mathematician, Floris Takens) was a way of envisioning a kind of order in turbulence. Could there be an attractor correlated to non-periodic, never-repetitive behavior? Geometrically stated, the problem was what kind of orbit could be drawn in a limited space so that it would never repeat or cross itself and which would produce an infinitely long line in a finite area. Interestingly, such a line would have to be fractal; however, at the time Reuelle and Takens claimed to have shown mathematically that such a line must exist, the notion of fractals had not yet emerged.¹⁹

But the concept of strange attractors and their presence in nature, their predictable unpredictability and novelty and their emergence at the boundaries of dynamical systems has become an important aspect of chaos theory. Their presence is related to new sensibilities about the difference in chaos and noise in their relation to information. The unpredictable spin-off of a system nested in the complexity and turbulence of our everyday world is not, as it were, "evil," that is, extraneous noise or static, but information fraught in its turn with apparently endless implications. At the heart of the so-called "butterfly effect" is the sense that every moment and every "turn" of a fractal is radically timeful in the sense that it is portentous with unforeseeable and inexhaustible import.

For Polanyi, just as we know more than we can tell, 
we also tell more than, in any explicit sense, we know.

William Shakespeare, with characteristic, almost numbing insight, has come close to summarizing a whole range of the issues here when, in Julius Caesar (III:3), he has Brutus say: "There is a tide in the affairs of men which, taken at the flood, leads on to fortune. Omitted, all the voyage of life is bound in shallows and misery. On such a full sea are we now afloat. And we must take the current when it serves or lose our ventures." It would appear now, not only from the biblical imagery, but from this new frontier in science, that some times, disanalogously to the rhythmic times of the ebb and flow of the ocean's tides, are a-rhythmic and, as such, far from being meaningless, they hold great promise. But because they are a-rhythmic they bespeak the essential nature of the particular moment in time as bearing within it a kind of now-or-never decisiveness which, in turn, bespeaks infinite possibility. It seems in the very nature of nature and history, as it were, to "sin boldly" - that is, to take risks and ventures and to live, if live they do, by grace, which is to say freely, but not thereby meaninglessly; or meaningfully, but not thereby deterministically.

Michael Polanyi and Non-Linearity

In light of these fairly recent developments Michael Polanyi's work seems strikingly prescient.²⁰ For Polanyi, just as we know more than we can tell, we also tell more than, in any explicit sense, we know. The telling to which we are heirs has set the stage upon which we receive our calling. However, what subsequently occurs upon the stage is not the theatrics of play-acting in which the lines have already been written, but action in that very sense without which we could not make any radical distinction between a John Gielgud playing Shakespeare's Hamlet and a John Kennedy acting the role of the president of the U.S.A. Our telling, in contrast to mere parroting, has as its conditions semantic dimensions which point beyond the explicit apparatus of the utterance both to the embodied speaker and to meanings, or if you will, to "strange attractors," which have been evoked and which evoke our being and our response, in a non-linear way. Polanyi's notion of "gradients of meaning" sloping in the direction of more stable configurations and, in a non-deterministic way, evoking our response, anticipates, but is enriched by, chaos theory's strange attractors and non-linear determinism.

For Polanyi, the ontological correlation of tacit knowing

 . . . consists not only in the fact that the known reflects the structure of knowing, but in the fact that it corresponds with knowing in a dialectical sense. Whatever is accredited as being real and/or true is, as such, embodied by the knower and the knowing process itself. . . . The truth becomes ever more "atoned," "attuned," "at one with," the way; ontology becomes epistemology. Epistemology expresses ontology.²¹

But the correspondence here is not the traditional, and therefore, perhaps the more obvious one in terms of which new accumulations of information simply become the objective factual foundation for an explicit and linear, deterministic process of inference making. "Rather, truth, incorporated and lived by the subject, takes on a life of its own and, accordingly, gains in its unspecifiable powers, insofar as it wholly outstrips any explicit control or deliberate manipulations."²² And at any given level of organization or comprehension the boundary conditions - though presupposing the earlier levels of integration - are left open by them.

This is Polanyi; however, here chaos theory is remarkably anticipated; and chaos theory extends and verifies what is implicit here. The feedback and iteration which chaotically generate order, which is then indwelled by the knower -- or, which, in ontological terms, is subordinated to a new level of emergence -- is a model of the non-linear way of emergence. Novel boundary conditions emerge in a non-linear and non-explicitable way in dialectic with prior conditions. No mere specification of subsidiary components and the laws which govern them explains or necessitates the comprehensive principle which subsumes them. The model of calling and evocation to which Polanyi had recourse receives reinforcement here; for clearly our acts of accrediting and placing at our disposal (indwelling) are functions of a sense of something being achieved which is irreducible to potential energy and specifiable deterministic processes. The movement toward new levels of integrations, epistemologically and ontologically, is clearly not as by necessity or destiny, but as by vocation, whose corollary is contingency.

As with the interpretation of quantum indeterminacy, arguments will persist as to whether the indeterminacy of so-called chaotic phenomena is ontological or only the result of momentary epistemological limitations. Indeed, some writers on chaos theory seem caught in this dilemma because they remain trapped in the very subject-object, mind-body dichotomy which Polanyi so effectively undermines. Chaos theory will also disarm this incredibly persistent mental set as we unpack the implications of quantum theory and chaos and of both to a theory of the "mindbody"²³ in its iterative, creative reflexivity and creative dialectical relation to "world." If someone wishes to say - in the vein of Einstein's response to Bohr and quantum theory - that the Lord God doesn't throw dice, that "nevertheless!" the consequent really and always is in the antecedent even if we can't predict it, one would want to say that this is Cartesian gnosticism; it is metaphysics in the vicious sense. Here language has gone on holiday.²⁴

Moreover, if the present does not entail the future and yet the future does not obtain without the present and the past, we must say not that the latter "causes" the former, but that the latter is contingently related to the former. That this way of speaking seems so unsatisfactory - no "explanation" at all - is due in large measure to the continuing presumption to explanation by way of recourse to the visual. We cannot visualize contingency for it is not a "thing" and is, therefore, elusive to visualization. Correlatively, we cannot create a graven image of time. We hear it and live it as it clings to us, but we cannot spectate it. In time it is no more the past which occasions the future than the future which occasions the past. The future bears down upon the present to create a new presence. The iterative relations of past and future generate chaos. They manifest real presence, the action of creation.

If there is time in this sense and if, therefore, we cannot "explain" the future from the past, then perhaps this is due to an energy or anti-entropy which ruptures any closure into the classical "pure" system, constantly relativizing it and giving "system" and time meaning.²⁵ Polanyi, as we know, said unequivocally, "I do not believe the universe is meaningless."²⁶ Wittgenstein said (in the Tractatus) that if there is any meaning to the world, it must lie outside the world. Perhaps this is so. But perhaps we should go on to say that meaning comes to us at the boundary, continually and freely changing it, though not in the manner of a meaningless, alien freedom which is in no way responsive to our own and to our history -- but perhaps in the manner of "chaos" as used here. The root analogy, I submit, is that of a dialogue leading us to unimaginable futures. It is this dialectical Judeo-Christian sensibility and fidelity to his own experience which emboldened Polanyi to write a book entitled Personal Knowledge.

©1992

NOTES

¹ Roche, Paul, (trans.) 1958. The Oedipus Plays of Sophocles, New York: New American Library.

² Poteat, W.H. 1985. Polanyian Meditations: In Search of a Post-Critical Logic, Durham: Duke University Press, p. 66. It should be noted that Poteat mounts a decisive critique of the notion that vision is timeless and "objective." However, the tradition, having obscured the phenomenon, has assumed that the "moment" of vision is without "temporal thickness."

³ See Poteat, W.H., 1956. "Tragedy and Freedom," The Carolina Quarterly, vol. VIII, p. 2. This paragraph is paraphrase and interpretation based on this article.

⁴ Ibid.

⁵ Ibid.

⁶ Ibid.

⁷ Ibid.

⁸ Gleick, James, 1987. Chaos: Making a New Science, p. 266. New York: Penguin Books. The following description of developments of chaos theory is everywhere indebted to Gleick's volume. See in addition: Paul Davies, 1988. The Cosmic Blueprint: New Discoveries in Nature's Ability to Order the Universe, New York: Simon and Schuster. For a more technical treatment of the subject see: Mandelbrot, Benoit, 1983. The Fractal Geometry of Nature, New York: W.F. Freeman and Co.; Thompson, J.M.O. and Steward, H.B., 1986. Nonlinear Dynamics and Chaos: Geometrical Methods for Engineers and Scientists, Chichester: John Wiley and Sons.

⁹ Ibid., p. 306.

¹⁰ Ibid., p. 250-251.

¹¹ Ibid., p. 251.

¹² Ibid., p. 121.

¹³ Figure 1 is adapted from A.E. Brotman's illustration. Ibid., p. 27.

¹⁴ Ibid., p. 27.

¹⁵ Ibid., p. 30.

¹⁶ Ibid., p. 30.

¹⁷ Ibid., p. 31.

¹⁸ Ibid., p. 228.

¹⁹ Ibid., p. 139.

²⁰ The reader who is unfamiliar with the works of Michael Polanyi is referred especially to Personal Knowledge: Towards a Post-Critical Philosophy, Chicago: University of Chicago Press, 1958; The Tacit Dimension, Garden City, N.Y.: Doubleday; and Meaning (with Harry Prosch), Chicago: University of Chicago Press, 1975. Polanyi's work was the focus of the March 1982 issue of Zygon: Journal of Religion and Science. (p. 17.)

²¹ Stines, J.W., 1985. "I Am the Way: Michael Polanyi's Taoism," Zygon: Journal of Religion and Science, vol. 20 (March), p. 66-67.

²² Ibid., p. 67.

²³ Poteat, W.H., 1985. Polanyian Meditations: In Search of a Post-Critical Logic, Durham: Duke University Press. In this and in subsequent works, Poteat has coined the term "mindbody" and given it force in his radical foray at undermining our persistent Cartesian dualism.

²⁴ Thomas Torrence has observed that this interpretation of Einstein is a widely-held misapprehension of Einstein's meaning here since Einstein clearly saw space-time relativity as undermining traditional views of causal connections. Clearly, that is important to note; however, it is the widely held misapprehension which is the relevant point here.

²⁵ The "anti-entropy" mentioned here is meant to suggest a freedom and/or transcendence which lies at the boundary of the "world" of the second law and its closure. It is a suggestion which is correlative to Kant's understanding of "world" as a limiting concept and to Wittgenstein's concept of the meaning of the world (if there is any) as lying outside the world. This does not mean that, for instance, somewhere within the world there is a perpetual motion machine. Surely, it is true to say that within the "world" of the second law there cannot be any relativizing "energy."

In addition (a different point) it seems entirely legitimate to raise a question about the sense in which laws may be said to continue to "hold" if the particular phenomena which they are presumed to cover are intractable to their predictive power. In certain respects, such laws seem to hold only in the Procrustean way linear reductions held for non-linear equations. They may well have powerful uses, but their philosophical import becomes more equivocal as the limitation on our knowledge of their future manifestations becomes more severe.

²⁶ Polanyi, Michael, 1958. Personal Knowledge, p. 286. Chicago: University of Chicago Press.