Science in Christian Perspective

On Cellular Automata and
the Origin of Life

John Byl

Department of Mathematical Sciences
Trinity Western University
Langley, B.C.
Canada V3A 6H4

In a recent issue of this journal Robert C. Newman presented a very interesting account of self-reproduction in cellular automata.¹ He was concerned particularly with a simple self-reproduction model that was developed by Christopher Langton .^2,3 Newman argues that Langton device is at or near the minimum complexity for self-reproduction of any meaningful form. He then goes on to argue that even for this very simplistic model of life, in the most favorable conditions, the chances of such a device occurring by chance are vanishingly small. Hence, since life itself is even more complicated, this amounts to very strong evidence that life is designed.

In this paper, we present a self-reproducing automaton that shares the basic features of Langton's model but is much simpler.

Langton's Automaton

For a detailed description of Langton's automaton we refer the reader either to Newman's account or to Langton's papers. What follows here is only a brief sketch.

In designing a machine that could reproduce itself, Langton considered a two-dimensional array of cells, each cell being in one of eight possible states. The state of each cell at any time is determined by the states of itself and its four nearest neighbors at the previous time-step.

Langton's device is shown in Figure 1. It essentially consists a signal that contains the information necessary to

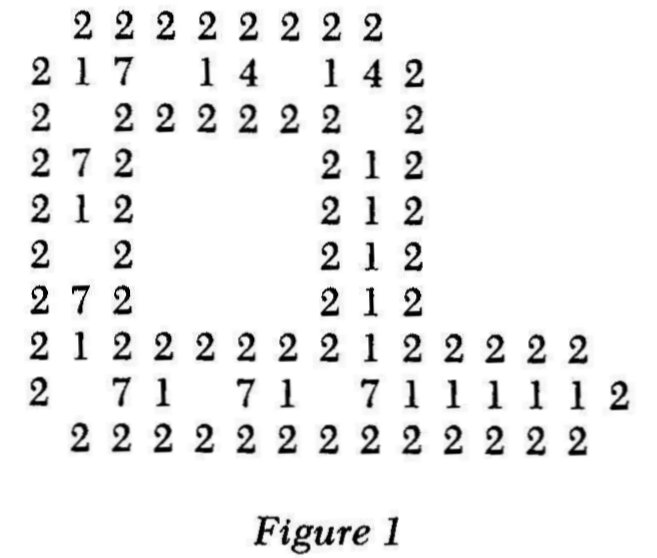
make a copy of itself, guided by two walls. The zero state (represented by a blank) is the quiescent state. States I and 2 guide the signal: I is an element of the data path, 2 is an element of the wall protecting the signal. The remaining five states are used as signals. To specify the direction of the signal, the digit following a signal is set to state 0. When a signal approaches a junction, it splits into two copies of itself, one along each path. The data path is lengthened by one unit when a 7-0 signal reaches the end; a left hand corner is made when two 4-0 signals hit the end in succession.

With these rules, and others for states 3, 5 and 6, the configuration shown in Figure I first extends its arm by six units. Then it turns left, adds another six units, turns left again, adds six more units, and turns left a third time. Then it closes in on itself States 5 and 6 are next applied to disconnect the new loop and to start the process over again. After 151 time steps we have two loops, each of which starts to form a new loop. The loops continue to reproduce themselves until all the available space is used up.

Newman estimates the complexity of this device by considering only those cells in the initial configuration which are in a non-zero state (86 cells) and only those transition rules that yield a non-zero state (190 rules). Assuming that all states are equally likely to arise by chance he finds that the number of possible random combinations is 7⁸⁶⁺¹⁹⁰, or 2 x 1 0²³². Since we have four possible rotations, this leads to a probability of one out of 5 x 10²³². that this automaton could arise by chance.

A Simple Automaton

The question arises whether the above automaton is indeed at or near the minimum possible complexity for self reproduction. In searching for simpler solutions, we will adhere to the criterion stated by Langton: we should take seriously the "self' of "self-reproduction," and require of a configuration that the construction of a copy should be actively directed by the configuration itself.²

Thus, we rule out trivial cases of "reproduction" that are generated solely by the transition rules. For example, we could construct a configuration where a cell could have one of two states (0 or 1) with two transition rules: a 0 surrounded by three 0's and 1 becomes a 1, and a 1 surrounded by three 0's and 1 becomes a 0. Then, starting with a 1 in a field of O's, the I will appear to reproduce itself (see Figure 2). But this we do not consider as self-reproduction.

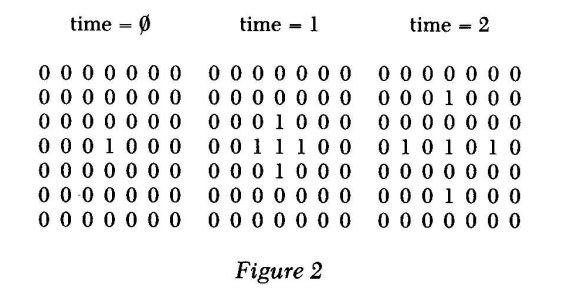
As stressed by Langton, we want to require that the responsibility for reproduction resides primarily with the parent structure. But not totally: the structure may take     advantage of certain properties of the "physics" of the interactions as this is represented by the transition rules.

Keeping these considerations in mind, we now present a simplification of Langton's automaton. The first modification is to eliminate the inner wall. The second simplification is to use just one 4-0 signal to make a left turn. The third change is to determine the direction of the signal not by an x-O combination, but by the orientation of each cell with regard to that neighboring cell having the lowest state. In order to ensure that this neighbor will normally be a segment of the outer wall, we assign the blank quiescent cells a numerical value of 7. Then we specify that, unless otherwise stated, the successor to states 3, 4, and 6 will be the state of the nearest cell clockwise from the smallest neighbor. The default for states 1, 2, 5, and 7 will be that the previous state remains unaltered.

The functions of the various states are as follows: state 2 refers to a segment of the wall, state I represents the segment of the wall at a junction (this is needed to keep the signal cycling within the configuration), state 3 defines the data path, 6 is used to add a unit to the data path, 4 forces a left turn, and state 5 is used to close the new loop and to initiate the formation of a further copy. Figure 3 shows a signal (i.e., 6634)  cycling inside the wall of a small configuration.

The numbering in this model is somewhat different from that used by Langton. This is partly due to the fact that the numbering is used to derive the orientation, and partly because we require only 7 states rather than the 8 used by Langton.

With these modifications it is possible to construct a simple initial configuration with only 12 cells which reproduces itself after 25 time-steps, as shown in Figure 4. The program used (based on Newman's program and written in

Quickbasic 4.0) is listed in the appendix.

After 25 steps, the original configuration and the daughter have the same form as the initial array. Then, as in the case of Langton's automaton, the daughter forms a new copy toward the right, while the original has turned 90 degrees and makes a copy toward the top of Figure 4. The process continues until all the available space is covered with copies.

The total number of transition rules used (see the program) is 36 plus the 7 default rules, for a total of 43. Applying the same Newman calculation as above, the number of random combinations of 12 cells and 43 rules of 7 possible states is 6¹²⁺⁴³ or 6 x 10⁴¹. Since there are at least 2 acceptable initial arrays (see time frames 0 and 24 in Figure 4) with 4 rotations each, the resultant probability is one out of 8 x 10⁴¹.

The Origin of Life

Newman estimates the probability of life occurring by chance as follows. Suppose that both the cells and transition rules in Langton's automaton correspond to atoms and that the different states refer to different elements (e.g., state I = carbon, state 2 = nitrogen, etc.). Then assume that all the atoms in a given volume of the universe are forming only 276-atom chains (86 cells plus 190 rules). Under the most favorable conditions, Newman estimates that there are in the entire universe at most 7 x IO" chains forming at a rate of 8 x 10¹¹ per second. The time to form 5 x 10²³² chains is then given by (5 x 10²³²)/((7 x 1071)(8 x 10¹¹))= 10¹⁴⁷ seconds, or 3 x 10^l39 years. On the basis of this immense timespan, Newman concludes that we have found very strong evidence that life is designed.

I wonder, parenthetically, whether this calculation is realistic. The main issue is whether the transition rules should be included in the probability calculations. I agree with Newman that a great part of the complexity is hidden in the transition rules. But should not at least a fraction of these rules be attributed to the operation of physical and chemical laws? Such laws can surely be assumed to be fixed and not determined by chance.

However, even if we grant the validity of Newman's probability analysis it is clear that his argument for design falls short. For on the basis of the simple (I 2 cell) automaton presented in this paper, the above form of calculation leads to a timespan of only 5 x 10^-43 seconds.

It must be stressed that life is considerably more complex than the simple mechanisms discussed in this paper. In fact, I suspect that Newman is right in his conclusion that the chance occurrence of life is virtually impossible. Yet, such conclusions must be founded on stronger evidence than that presented by Newman. Such evidence does exist: more sophisticated calculations indicate that, on the basis of currently known physical laws, the probability of life arising spontaneously is extremely small.⁴

^®©1989

REFERENCES

¹Robert C. Newman, "Self-Reproducing Automata and the Origin of Life," Perspectives on Science and Christian Faith 40 (1988):24-3l.

²Christopher G. Langton, "Self-Reproduction in Cellular Automata," Physica 1OD (1984):134-144.

³Christopher G. Langton, "Studying Artificial Life With Cellular Automata," Physica 22D (1986):120-149.

⁴See, for example the calculations of E. Argyle, "Chance and the Origin of Life," Origins of Life 8 (1977):287-298; H. P. Yockey, "A Calculation of the Probability of Spontaneous Biogenesis by Information Theory," Journal of Theoretical Biology 67 (1977):377-398.