Determinism and Chaos

Determinism and Chaos

Richard H. Bube
Department of Materials Science & Engineering
Stanford University
Stanford, CA 94305

From: Perspectives on science and Christian Faith 41 (December 1989)

The nature of the interaction between "determinism" and "chance" has been the subject of continued debate in one form or another from the early days of recorded human thought. Theologically, it is well known as the "predestination vs. free will" debate, although the actual connection between the theological debate and the scientific debate is tenuous at best. The development of science in the last few centuries has given it a new intensity, since scientific descriptions must fall either into the category of deterministic or chance (probabilistic), neither of which as an isolated world view is compatible with biblical concepts of human responsibility. A thumbnail sketch of the question and its implications has recently been given in this journal.¹ I believe it is fair to say that evangelical Christians with a commitment to both authentic science and authentic biblical theology largely follow the lead of those like MacKay who maintain the existence of a reality in which both determinism and chance are intricately and sometimes even mysteriously interrelated.²

A curious and fairly dramatic twist to this debate has been given in recent years by the scientific recognition of the state known as "chaos." In the popular mind, chaos is what one would expect in a completely random or chance-oriented environment; we have been delivered from chaos by the existence of order (deterministic relationships). Some of the early ideas of creation dealt with God's overcoming chaos with order, again emphasizing the common expectation that these two kinds of description are mutually exclusive.

The contention that we ought to expect complex interactions between determinism and chance, or between order and chaos, has found a rather dramatic expression in recent discovery of those specific effects that have come to be known as "chaos." It is the purpose of this communication to illustrate the type of effect observed (in one of its simplest manifestations).

A recent insert, in Science magazine, entitled "A Simple Model of Chaos,"³ describes a model based on population biology that illustrates nicely how "chaos" can proceed from a deterministically described process. The population of a particular insect species in one year N_t is related to the population in the following year N_t+1 approximately by the following relation:

N_t+1 = alphaN_t(1 - N_t) (1)

Here N_t is expressed in appropriate units so that its numerical values fall between 0 and 1 (a negative value for 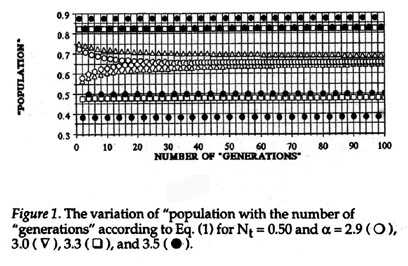N_t+1 would imply extinction), and alpha is a constant that controls the specific form that the results of Eq. (1) take over a number of generations. In order to express the implications of Eq. (1) it is necessary to choose a value for alpha and an initial value for N_t. It is the extreme sensitivity of Eq. (1) to small variations in the initial value of N_t for certain values of alpha that characterizes chaotic behavior.

Figure 1 shows the variation of the "population" with the number of generations from 1 to 100, for values of alpha between 2.9 and 3.5, and an initial value of N_t = 0.50. It can be seen directly from Eq. (1) that if alpha = 2.0 when N_t = 0.50, N_t+1 = N_t, and the population is unchanged with successive generations. When alpha = 2.9, early generations show alternating values which quickly decay down to a "population" of about 0.65 within 20 to 30 generations. When alpha = 3.0, the decay of the two alternating values is much slower and persists out to 100 generations, so that the 99th generation shows N_t = 0.68 and the 100th generation shows N_t = 0.64. When alpha = 3.3, there are again two alternative values (0.82 and 0.47) but these are stable in alternate years over the range from 1 to 100 generations. When alpha = 3.5, the number of alternative values (0.87, 0.82, 0.50 and 0.38) jumps to four, and these are unchanging from 1 to 100 generations. Although these four cases show increasing complexity, they also give the appearance of an ordered and structured complexity.

When alpha = 3.57, this ordered behavior gives way to chaos. The data points in Figure 2 show the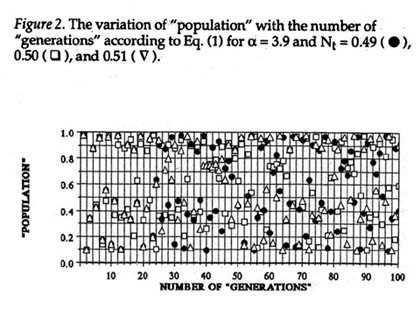 "populations" for alpha = 3.9 and for three cases in which N_t = 0.49, 0.50 and 0.51, three numbers differing by only 2% from one another. Right from the first generation on, the points jump around in a random fashion. For the first 10 generations the points for the three different initial values of N_t are approximately the same, but after 20 or 30 generations, major differences between the three sets of data arising from different initial values of N_t are evident. Table 1 lists the specific "population" values shown in Figure 2 for a few selected later generations, showing the very strong influence of the small difference in the initial values of N_t.

These results illustrate how the condition of chaos can be generated from a deterministic relationship. Counter 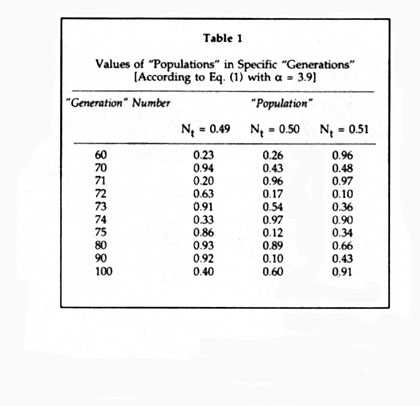examples are also available that show how an orderly pattern or structure can be obtained from a large set of random events suitably limited by appropriate boundary conditions: the generation of order out of chaos. There is no necessary profound philosophical or theological implications in these results, but they do warn us to avoid simplistic dichotomies between deterministic and chance processes as we face interactions between science and theology.

NOTES

¹R.H. Bube, "Penetrating the Word Maze: Determinism/Chance," Perspectives on Science and Christian Faith, 41, March (1989), p. 37.

²D.M. MacKay, The Open Mind and Other Essays: A Scientist in God's World, edited by Melvin Tinker. (Leicester, England: Inter-Varsity Press, 1988).

³R. Pool, "A Simple Model of Chaos," Science 243, 311 (1989).