Science in Christian Perspective

MAC KAY'S ARGUMENT FOR FREEDOM
A Pictorial Representation of MacKay's Argument for Human Freedom in a Mechanistic Universe
John A. McIntrye
Physics Department, 
Texas A&M University College Station, Texas 77843

From: JASA 33 (September 1981): 169-171.

Some twenty five years ago, Donald M. MacKay proposed a novel argument which allowed, on the one hand, the freedom of men to determine their own actions even though, on the other hand, everything in the universe was assumed to be mechanistically determined.¹ Perhaps as remarkable as the argument itself, is the confusion that it has produced. A considerable literature has been developed concerning the argumentl^2-4 and in his book, The Clock Work Image,³ MacKay has devoted an Appendix to listing and answering seventeen objections to his argument. Furthermore, in this Journal, there was recently an exchange between MacKay and John Cramer concerning the argurnent.⁵ As a contribution toward understanding the essence of MacKay's argument I wish to present here a statement of his argument in graphical form. With the argument thus laid out in a pictorial format, the mind can visualize as well as analyze the argument as it is unfolded.

With the brain state at any instant of time now described as numbers we can obtain a visual description of the brain by plotting the numbers against coordinate axes. In Fig. 1, for example, we

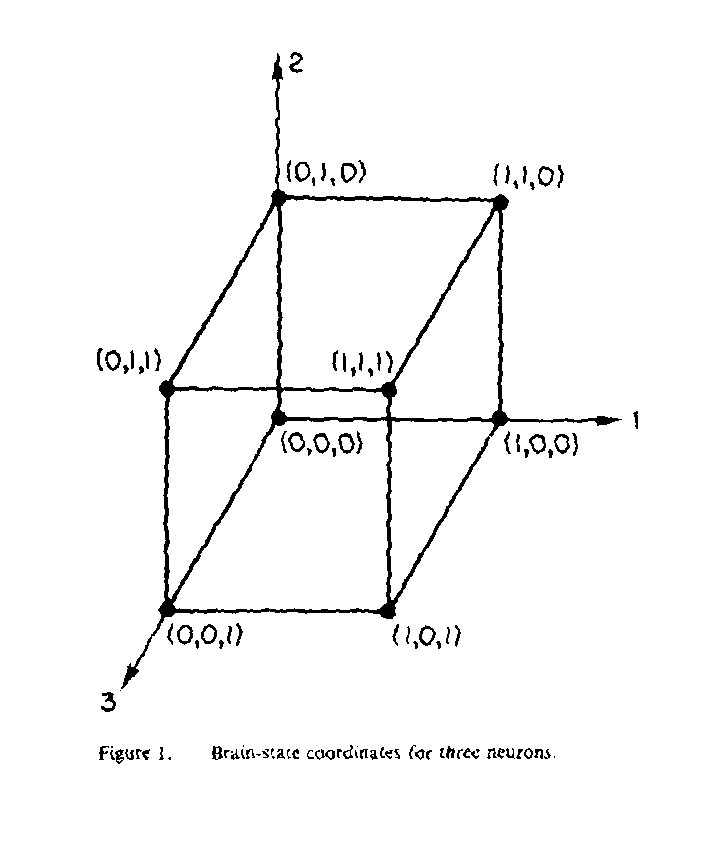
have a plot for a brain containing only three neurons. Each of the three coordinate axes represents one of the three neurons, and the 21 = 8 dots indicate the eight possible states of the 3-neuron brain. The numbers in the brackets give the coordinates of the dots and correspond to neurons 1, 2, and 3 respectively. Thus the brain coordinates indicated by (0, 1, 1) correspond to a brain state where neurons 2 and 3 are active and neuron I is inactive. Furthermore, as time goes by, the state of the brain changes so that a dot representing the brain state in Fig. I moves to a new location. The activity of the brain can be described, then, by the path of a dot in Fig. I as it moves with time.

Since we are discussing the state of the brain as it changes with time, it is convenient to plot the brain state against a time axis. However, the brain state in our example has three dimensions (coordinates), and three dimensions cannot be plotted against a fourth dimension time. Thus, we must be content with a schematic plot (Fig. 2) where all of the brain coordinates are represented by the vertical axis.

In principle, it is easy to generalize from 3 neurons to n neurons in the brain. There will then be n coordinates (instead of 3 coordinates) in Fig. I and 2n points in the plot. (Such a plot, of course cannot be represented in our 3 dimensional world). However we can still conceive the state of the brain at any instant as being one point in this dimensional plot. And finally, as before, we can represent schematically the n coordinates as a single vertical coordinate in the time plot (Fig. 2). Thus, we can represent schematically the physical (and conscious) state of a brain by a curve having the coordinate axes of Fig. 2. For reference, we denote a representation of a brain using the brain-state coordinates plotted against time as a brain-state diagram.

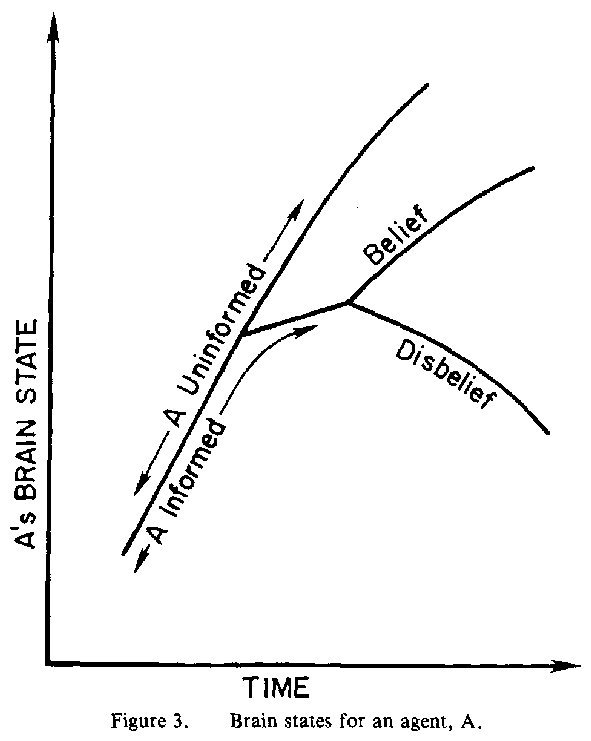
Laplace's super-Intelligence who uses the deterministic laws of the natural world to completely predict the future.) The state of A's brain according to this prediction (of which A is uninformed) is represented by the curve "uninformed" in a brain-state diagram (Fig. 3). Thus A's brain state follows deterministic laws and A's future conscious behavior can be completely predicted by B.

We now introduce the possibility that B informs A of his prediction of the future of A's brain-state. Then, the original prediction will no longer be valid and A's brain state will be represented by a curve denoted "informed" which branches away from the "uninformed" curve. (Of course, B, in his omniscience, will modify his prediction of A's future brain state to allow for the fact that A now knows the prediction).

Now among the different effects of A's knowledge of the prediction on his brain will be the requirement for A either to believe or disbelieve the prediction. Since B has complete predictive power of A's deterministically-controlled brain, B can predict A's future brain state either if (1) A believes B's prediction of A's brain state or if (2) A disbelieves the prediction. Thus, if A were to believe B's prediction of A's brain state, B will predict that A's brain state will follow the "belief" curve (Fig. 3); if A were to disbelieve B's prediction of A's future brain-state, B will predict that A's brainstate will follow the "disbelief" curve (Fig. 3).

Furthermore, the observer B can predict whether A will indeed believe or disbelieve. To justify this statement in an objective manner, let us suppose that A has previously decided to make all of his "believe" decisions by flipping a coin with the consequence of "heads, I believe; tails, I disbelieve". Because the result of the coin flip depends on physical factors of which B is aware, B also knows whether A will believe his prediction about A's future brain (If A decides to believe on grounds other than a coin flip, B also, of course, know whether A will believe because A's brain functioning in a deterministic fashion).

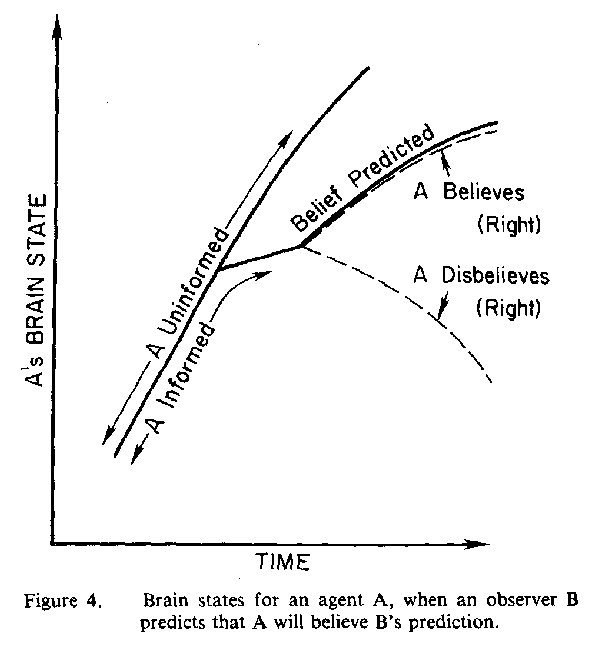
We now consider the case when A believes B's prediction. Since B knows that A will believe, he predicts the "believe"' curve (( line in Fig. 4). We next consider whether A himself has a logically free choice to believe or disbelieve this prediction (even though and observer B, know that A will believe). If A believes the prediction, he is right since his brain will follow the "belief" curve predicted (upper dashed curve in Fig. 4). If A chooses to disbelieve B's prediction, he would also be right because, then, his brain stale would follow the "disbelief" curve (lower dashed curve in Fig. 41 and the prediction would be in error. In this case then, A has the logical freedom either to believe or to disbelieve (and to act accordingly) because he would not be wrong if he did either one.

We must consider the case where B predicts (correctly) that A will disbelieve B's prediction of A's future brain state (solid line in Fig. 5). In this case, if A believes the prediction, his brain state will follow the upper dashed "believe" curve in Fig. 5. Consequently. A would be wrong to believe the prediction since the "believe" curve does not coincide with the predicted solid curve. On the other hand, if A disbelieves the prediction, his brain state win follow the lower dashed "disbelieve" curve in Fig. 5. This time, A would still be wrong to disbelieve the prediction since now the prediction is correct (the lower dashed curve agrees with the predicted solid curve). Thus if B's knowledge leads him to predict (correctly) that A will disbelieve his prediction, A would be in error either to believe or to disbelieve B.

Summarizing these results, we have, in the second case, the conclusion that A will be in error (wrong) whether he believes or disbelieves the correct prediction. In the previous case we had the conclusion that A would be correct (right) whether he believes or disbelieves the correct prediction. Thus, in neither case, does B's prediction have, in MacKay's words,⁶ "an unconditional claim to A's assent,"

Except for predictions about the brain state of the person A (agent) under discussion, the (granted) determinism of the physical world does restrict personal freedom of choice. To take an example of MacKay's, if B informs A of a (correctly) predicted eclipse, the agent A, as well as the observer B, would be right to believe the prediction and wrong to disbelieve the prediction. In this case, B's prediction does have an "unconditional claim to A's assent" and A would not have the freedom either to believe or disbelieve the prediction, i.e. A does not have a freedom of choice about believing the occurrence of an eclipse.

However, as we have seen in the discussion above, if B tells A what A is going to do (A's action, of course, being determined by A's brain-state) then B's prediction no longer has "an unconditional claim to A's assent." Thus, while B's prediction will always be correct (since we granted B the power of prediction in a mechanistic universe), nevertheless, A will not be forced logically to accept B's prediction. For, in Case I above (Fig. 4) A will be right whether or not he believes B's prediction while, in Case 2 (Fig. 5) he will be wrong whether or not he believes B's prediction.

However, the reader may well object that most of the time no one is telling A what he is going to do. Rather A is making his choices independent of an observer B. In this situation, in both Figures 4 and 5, A's brain state follows the "uninformed" curve. This curve is predictable by an observer B and is unaffected by any effect of B's predictions since A is not informed about the predictions. In fact, B can write down what A will do and, after A has performed according to prediction, B can show A that B has been able to predict all that A did.

On this basis B might tell A that A had no freedom of choice. However, A can be stubborn and still insist that, during the course of his actions, he was making free choices. To adjudicate their disagreement, A and B can decide to take their case to what MacKay' calls, a "logical court." The court is asked to decide whether A had freedom of choice even though B was able to

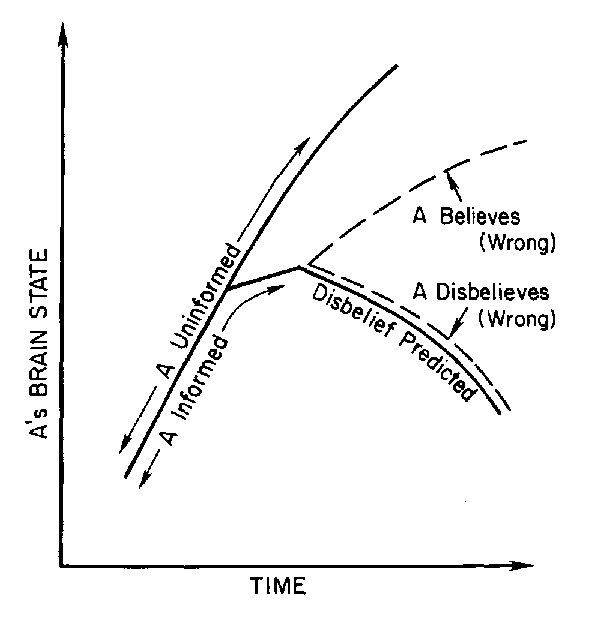
Figure 5. Brain states for an agent A, when an observer B
predicts that A will not believe B's predictions.

predict all of A's actions beforehand. To make its decision, the court uses the test: did B's prediction of A's actions have "an unconditional claim to A's assent?" In performing this test, the court must consider the logical status of A's brain state if A had been informed of B's prediction (although A need not be informed to make this logical test). Thus, when the court tests B's predictions A's brain states in Fig. 4 and 5 will leave the "uninformed" curve and proceed along the informed curves even though, while he was making choices, A's brain state had followed the "uninformed" curve. Consequently, in following the "informed" curves, the court will uncover the logical peculiarities associated with these curves (as discussed above) and the court will rule that B's predictions did not have "an unconditional claim to A's assent" even though, while A was acting, A was unaware of B's predictions. Thus, A has a logical freedom of choice at all times whether or not he is informed of (correct) predictions concerning his future actions.

In summary then, A, the agent, has the logical freedom to choose even though B, the observer, can predict everything that A will do. This freedom of A's is independent of whether or not B informs A of his predictions.

The author has benefited from correspondence with Dr. MacKay.

¹MacKay D.M., "On Comparing the Brain with Machines." The Advancement of Science 40: 402-406, 1954; American Scientist 42: 261-268, 1954; Annual Report of Smithsonian Institute: 231-240, 1954.

²MacKay D.M.: "Choice in a Mechanistic Universe: A Reply to Some Critics." The British Journal of the Philosophy of Science 22: 275-285, 1971, and references therein.

³MacKay D.M.: The Clock Work Image, Inter-Varsity Press, Downers Grove, IL, 1974. Human Science and Human Dignity, Inter-Varsity Press, Downers Grove, IL, 1977.

⁴Christian Scholars Review, 1978: Hasker W., "MacKay on Being a Responsible Mechanism: Freedom in a Clockwork Universe:" 130-140; MacKay D.M., "Responsible Mechanism or Responsible Agent? A response to William Hasker:" 141-148; Hasker W., "Reply to Donald M. MacKay:" 149-152.