Science in Christian Perspective

Truth : Mathematical and Biblical
DAVID L. NEUHOUSER
Dapartment of Mathematics
Taylor University
Upland, Indiana 46989

From: JASA 31 (March 1979): 29-33.
Presented at the 1976 Annual Meeting of the ASA at Wheaton College.

Is the statement, "You can't prove that God exists" true or false? Of course, the meaning of the words is of crucial importance in attempting to answer that question. In particular, there are two eligible, and quite different, meanings for the word "prove." One definition for the word "prove" would he the usual definition that mathematicians use. A second would he a logical argument which would convince every sane per
son. As we shall see, these two definitions are not the same at all.

Basic Assumptions 

In every mathematical system certain statements are assumed to be true. These assumptions are called axioms or postulates. To see why it is necessary to have assumptions, (i.e., why it is impossible to prove every statement) consider the following. To prove that statement, Si, is true we must give a statement, S2, as a reason. Then to prove that S2 is true we must give another reason S3. This process must either continue indefinitely, be circular, or at some point come to a statement which we say is one of our basic assumptions. So in mathematics we prove statements (called theorems) by starting with axioms and using logic or deductive reasoning. We are then certain that our theorems are true if our assumptions are true. But if our assumptions are in doubt, then we cannot be certain about our conclusions. We cannot use deductive reasoning to prove that our axioms are true, because as we have seen, every mathematical system must start with some assumptions. Therefore, in mathematics we can never arrive at certainty. In fact, it's even worse: mathematicians are not even interested in whether or not a set of axioms is true. They ,would he happy if they could just show that they are consistent. Even here they have trouble.

Kurt Godel, a mathematical logician, demonstrated in 1931 that if you have a set of axioms that's complete enough to give such a simple thing as the real number system, then it cannot be proved to be consistent. Notice that he did a very interesting thing. Only mathematicians do these kinds of things. He proved that it is impossible to prove that a set of axioms is consistent.

Now, of course, we believe that they are consistent, but that is exactly the point I'm trying to make. We are reduced to the place where we must have faith. We cannot prove it. In fact, we even prove that we can't prove it.

Suppose we loosely define a religion as any discipline whose foundations rest on an element of faith , . there may or may not be reason present, but at least there has to be some element of faith. Quantum mechanics, for example, would be a religion tinder this definition. But mathematics would hold the unique position of being the only branch of theology possessing a rigorous demonstration of the fact that it should he so classified.¹

So, in the first sense of the word "prove," we can prove that God exists. We just have to start with the right assumptions. But these assumptions may be in doubt, in which ease the "proof" doesn't mean anything. In the second sense of the word we cannot prove that God exists, but we cannot prove (in this second sense of the word) that God doesn't exist either.

Mathematical proof, then, consists of going from axioms to theorems by way of deductive reasoning. Axioms are sometimes called postulates or assumptions, and when this method is used in science they may be called hypotheses, presuppositions, and sometimes even laws. Today a set of assumptions used in science is often called a model. It is important to note that deductive reasoning cannot lead its to these axioms. Then what good is deductive reasoning? I believe there are at least two very important things that reason does for us.

I. If through observation, experience, revelation, or any other method see come to believe something, then reason can he used to deduce other things (let's call them conclusions). That is, if our hypothesis is true, 
then our conclusions are true also and we have become (Aware of new truths or at least truth in a new end per/saps more useful form.
11. The conclusions can be used to test the original hypothesis. If the conclusions (Agree with our experience, we have even snore faith in our hypothesis. But, if the conclusions do not agree with our experience, our faith in the hypothesis may be weak-cued or even destroyed.

Mathematical Method and Divine Revelation

Now, let us consider how the mathematical method (i.e., deductive reasoning), the scientific method, and faith in divine revelation are related. As first it would seem that revelation and the scientific method have nothing in common. However, when we consider the question, "Is a particular proposition or set of propositions a divine revelation?" it sounds a lot like the question, "Is a particular proposition or set of propositions a good scientific model or theory?" Perhaps there is some similarity in the way we might answer these questions. Before attempting an answer let us consider
the scientific method.

There may not even be such a thing as the scientific method. There are certainly different methods or procedures in different sciences. For example, in some parts of astronomy, geology, and biology the important method of repeated experiments is not possible. Even so, I believe (note that at least an element of faith is now a part of this paper even if evidence of learning never appears) there are some things common to all scientific investigation. From my background in mathematics, I feel free to define the scientific method to be some of these common elements.

In order to find these common elements, we start by looking at a popular, and over-simplified, description of the scientific method. A scientist gathers and organizes data. He then uses inductive reasoning to make generalizations. Since I am a mathematician, I will call these generalizations postulates. These postulates are checked against all the data possessed by the scientist and new experiments may he designed to test the generalizations further. These postulates may he used as premises and by means 0f deductive reasoning further generalizations (or theories) can be derived. These, of course, can be tested in the same way as postulates. At each testing new data are obtained and the cycle of steps repeated. It is the scientist's belief that, in the long rut), this procedure gives closer and closer approximations to the truth about reality. Figure 1 illustrates this procedure.

{inexact representation of Fig 2.}

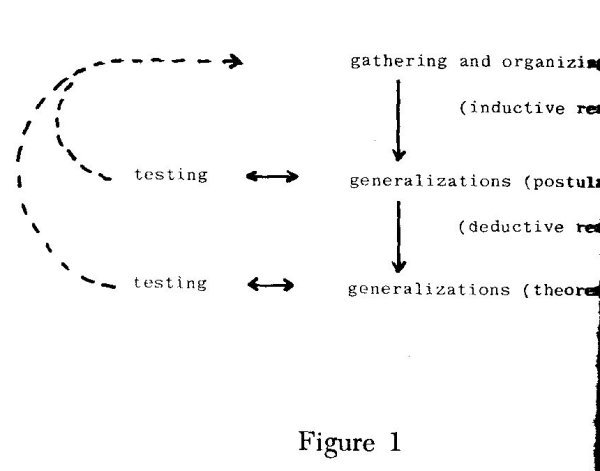
g data

asoning

ates

asoning

As an example of this, Isaac Newton observed various falling bodies (including apples and the moon). From these data he hypothesized that there is a force of attraction between every two objects which is directly proportional to the product of their masses and inversely porportional to the square of the distance between them. From this he could deduce Kepler's Law's of planetary motion and many other relations. Newton himself believed that this was the way the scientific method operated. In spite of Newton's belief, there seems to me to he one serious flaw in the whole scheme and that is the step where he went from the data to the formula by induction alone. It is certainly clear that Newton did go from the data to the formula, but 1 think that there must he more involved than inductive reasoning. Figure 2 is a modification of Figure 1 which shows some of these extra things. Please notice particularly the last of the added elements.

{inexact representation of fig 2., ed.}

         ^
         |
         |
         |

 
 testing
     ^
      |      |
      |
   testing

Before commenting further on these additions to the scientific method, it should be pointed out that the scientist does not begin at the top of these diagrams with a completely open or unbiased mind. He has various presuppositions, attitudes, arid inclinations determined by his culture, psychological make-up, and overall vision of the world. It is also possible, and even probable, that his participation in the scientific endeavor will modify these.

Physicist Werner Heisenberg said, "In fact, imagination plays a decisive role in natural science. For even though we can hope to get at the facts only after many sober and careful experiments, we can fit the facts themselves together only if we can feel rather than think our way into the phenomena."² Einstein would even say that Figure 2 is not just a modification of Figure 1 but a totally different process. In his view,

the best path to be followed might not be that of observation followed by induction of general laws, but the totally different process of postulating a theory and then discovering whether or not the facts fitted it. Thus a theory should start with more scientific and philosophical assumptions than the facts alone warranted.²

One of these assumptions was his belief in the harmony of the universe.

Therefore, perhaps a better way of looking at the scientific method would he to call the set of postulates a theory or model. This model is obtained in some way from data by means of induction, imagination, inspiration, etc. It seems to me not unlikely that at times

Revelation is a gift to us from God, but our evaluation of it and acceptance of it may be a result of a reasoning process very much like the scientific method.

God gives some revelation of a scientific nature to a scientist, whether the scientist is a Christian or not. He works in mysterious ways his wonders to perform. In whatever way this model is obtained it is essential that reason he used to determine whether or not it is acceptable. It must he checked against all kinds of evidence. It will probably seem to he in conflict with some of the evidence. This usually is a surprise to most nonscientists. The scientist does not discard a model just because it contains some paradoxes. He compares it with other models. None will be able to explain everything. All will probably involve paradoxes. None can be proved by a single line of reasoning, so cumulative evidence is important in determining in which of the various models the scientist places his faith. From this time on, the behavior of the scientist will depend, at least in part, on which model he believes in and the degree of that belief.

How then does this relate to divine revelation? Suppose you receive what you think is a divine revelation. How do you know, in fact, that it is a revelation and not just the result of an idea planted in your subconscious mind from the combination of a television show you saw last week and a dream you had last night, perhaps aided by a touch of indigestion or the sight of a beautiful sunset? I think we would have to use the same kind of testing we use for a scientific theory. John Locke put it this way,

Whatever God bath revealed is certainly true: no doubt can be made of it. This is the proper object of faith: but whether it he a divine revelation or not, reason must judge , . . God when He makes the prophet does not unmake the man . . . I do out mean that we must eonstilt reason and examine whether a proposition revealed from God can be made out by natural principles and if it cannot then we may reject it: but consult it we must.⁴

Even Jeremiah was not always sure when he had received a revelation until he checked it against the evidence. Jeremiah 32:6 and 7 says, "and Jeremiah said, The word of the Lord came unto me, saying, Behold, Hanameel the Son of Shallum thine uncle shall come unto thee, saying, Buy thee my field that is in Anathoth: for the right of redemption is thine to buy it." Verse 8 tells how his uncle came with the offer to buy the field and Jeremiah says, "Then I knew that this was the word of the Lord."

In Matthew 11 we have another example of this type of testing of faith. Keep in mind that the incidents reported in this chapter occurred after John the Baptist's declaration to the crowd on the occasion of the baptism of Jesus, "Behold the Lamb of God, which taketh away the sin of the world." Now John sends his disciples to inquire of Jesus, "Art thou he that should come or do we look for another." Jesus does not costdemo John for his lack of faith, in fact, he praises him as a prophet saying, "Among them that are born of women there bath not risen a greater than John the Baptist." The answer Jesus gives is that they should look at the evidence. "The blind receive their sight, and the lame walk, the lepers are cleansed, and the deaf hear, the dead are raised up, and the poor have the gospel preached to them."

The Greatest Model

Now let us consider the greatest revelation of all and the greatest model of reality, namely the biblical or Christian view of reality. We may not he able to use reason to arrive at this biblical view of reality, but we can use reason to check it. Note also that we can say the very same thing about Einstein's Theory of Relativity; we may not be able to use reason to arrive at it but it can be checked by the use of reason. Following is a list, although certainly not a complete list, of some of the types of evidence for the biblical or Christian vie" of reality.

1. The existence of moral low.
2. The truth of the biblical statements that con be verified.
3. Historical evidence of biblical events.
4. Personal experience and the personal experience of other Christians.
5. Scientific evidence.
6. The weaknes of alternative (i.e., non-Christian) models.

C. S. Lewis' book, Mere Christianity, discusses the existence of moral law biblical statements that
as evidence, there are many can be checked by our experience or the results of natural or social science. None of These Diseases by Dr. S. I. McMillan looks at many of God's commands to the Israelites in the light of modern medical knowledge. History and Christianity by John W. Montgomery is a good hook on historical evidence. The fourth point in the list may not sound like part of the scientific method, but Heisenherg said, "science, too, is based on personal experience, or on the experience of others reliably reported."⁵ One example of scientific evidence is William Pollard's thesis, elaborated in Chapter 4 of Physicist and Christian that every path of investigation of nature leads to supernature. Many of C. S. Lewis' books (e.g., Miracles and The Abolition of Man) discuss various types of evidence. Perhaps none of these paths alone is convincing to a given individual, but remember that the same thing was true in the scientific method. The power of cumulative evidence is the really important point here.

There are paradoxes in this model; for example, man's free will and God's sovereignty, God's justice and mercy, and human suffering and God's love. We can't overlook these problems, but paradoxes do not necessarily overthrow the model.⁶ There are extremely difficult paradoxes in the mathematical system of real numbers, but all the mathematicians I know have a great deal of faith in it. Physicists cannot reconcile the wave and particle nature of light, but they believe in both. Whether the paradoxes in the biblical theory of reality are enough to overthrow a person's faith depend upon the strength of the cumulative evidence and the weakness of the alternative models. Atheism, for example, has the problem of trying to answer the questions of how personality can he produced by an impersonal universe or how love and care can come from an unloving and uncaring universe. As Elton Trueblnnd has said,

"A believer believes in God partly because he is unable to make a leap of faith as great as the atheist is forced to make."⁷

My conclusion is that the process of understanding and coming to have faith in divine revelation is very much similar to the process of understanding and coming to have faith in a scientific model. I realize that revelation is a gift to us from God, but our evaluation of it and acceptance of it may be a result of a reasoning process very much like the scientific method. We should remember that scientific models are obtained in various ways, perhaps even sometimes by revelation, but, in any case, must be checked by the procedures in the scientific method. In my opinion, we tend to overestimate the role of reason in science and underestimate the role of reason in religion. Bertrand Russell, one of the greatest mathematical logicians said,

there is an clement of truth to be learned from the mystical way of thinking (revelation, insight, intuition) which does not seem to be obtained by any other manner
What I do wish to maintain-and it is here that the scientific method is imperative-is that insight, untested and unsupported is an insufficient guarantee of truth, in spite at the tact that much of the most important truth is first suggested by its means.⁸

This relationship is stated by the theologian, J. Edward Dicks, in this way,

reason can become effeeive only when it is supplied material that is given it by faith. The relation is one of reciprocity. Reason contributes as it makes a critical analysis of faiths, tests its premises, interrogates its criteria, and holds in check its tendency to resort to authority.9

Perhaps, you are not conscious of this sort of process in your own experience. It is my belief that consciously or unconsciously you use reason in some of the ways I have described. If not, as Pascal has said,

Therefore, those to whom God has imparted religion by intuition are very fortunate and justly convinced. But to those who do not have it, we can give it only by reasoning, waiting for God to give spiritual insight, without which faith is only human and useless for salvation.¹⁰

I believe that for some people, at least, reason plays an important role in coming to faith. Reason cannot lead a man to God, but it can lead him to a position where God is able to reveal himself to man. Therefore, for many reasons, I agree with J. Edward Dicks' statement that "a faith accepted by critical analysis by reason is better than a faith Goddled to avoid contact with reason."¹¹ Also, I agree with the biochemist, Denis Alexander, that "The revelation of God in Christ is accepted because as a general model of explanation it 'fits the facts' about the human condition in a way that no other model does."¹²

REFERENCES

¹Evcs, Howard and Ncwsom, Carroll. An Introduction to The Foundations and Fundamental Concepts of Mathematics. N.Y.: Holt, Rinehart and Winston, 1966, 305.
²Heisenberg, Werner. Physics and Beyond. N.Y.: Harper and Row, 1972, 186.
³Clark, Ronald W. Einstein: The Life and Times. World Publishing Co., 1971, 94.
⁴Miller, Ed. L., ed. Classical Statements on Faith and Reason. N.Y.: Random House, 1970, 105, 113.
⁵Heisenherg, 216.
⁶Again C. S. Lewis is helpful in the understanding of some of these problems, in particular The Problem of Pain and also his novel Till We Have Faces, The latter sheds light on the paradox of justice and mercy.
⁷Trueblood, Elton. A Place to Stand. N.Y.: Harper and Row, 1969, 20.
⁸Russell Bertrand. Mysticism and Logic. London: Allen and Unwin, Ltd., 1959, 9, 12.
⁹Von Crueningen, John Paul, ed. Toward a Christian Philosophy of Higher Education. Westminster Press, 1957, 59.
¹⁰Pascal, Illaise. Pensees. 282. 
¹¹Von Crueningen. 60.
¹²Alexandcr, Denis. Beyond Science. N.Y.: A. J. Holman Company, 1972, 182.